🪢 Cette nouvelle approche de la théorie des cordes pourrait enfin expliquer notre Univers
Restez toujours informé: suivez-nous sur Google Actualités (icone ☆)
Les prédictions de la théorie des cordes conventionnelle sont incompatibles avec l'observation de l'énergie noire, qui semble accélérer l'expansion de notre Univers. Elles ne s'accordent pas non plus avec les théories viables de la gravité quantique, prédisant plutôt un vaste 'marais' d'univers impossibles.
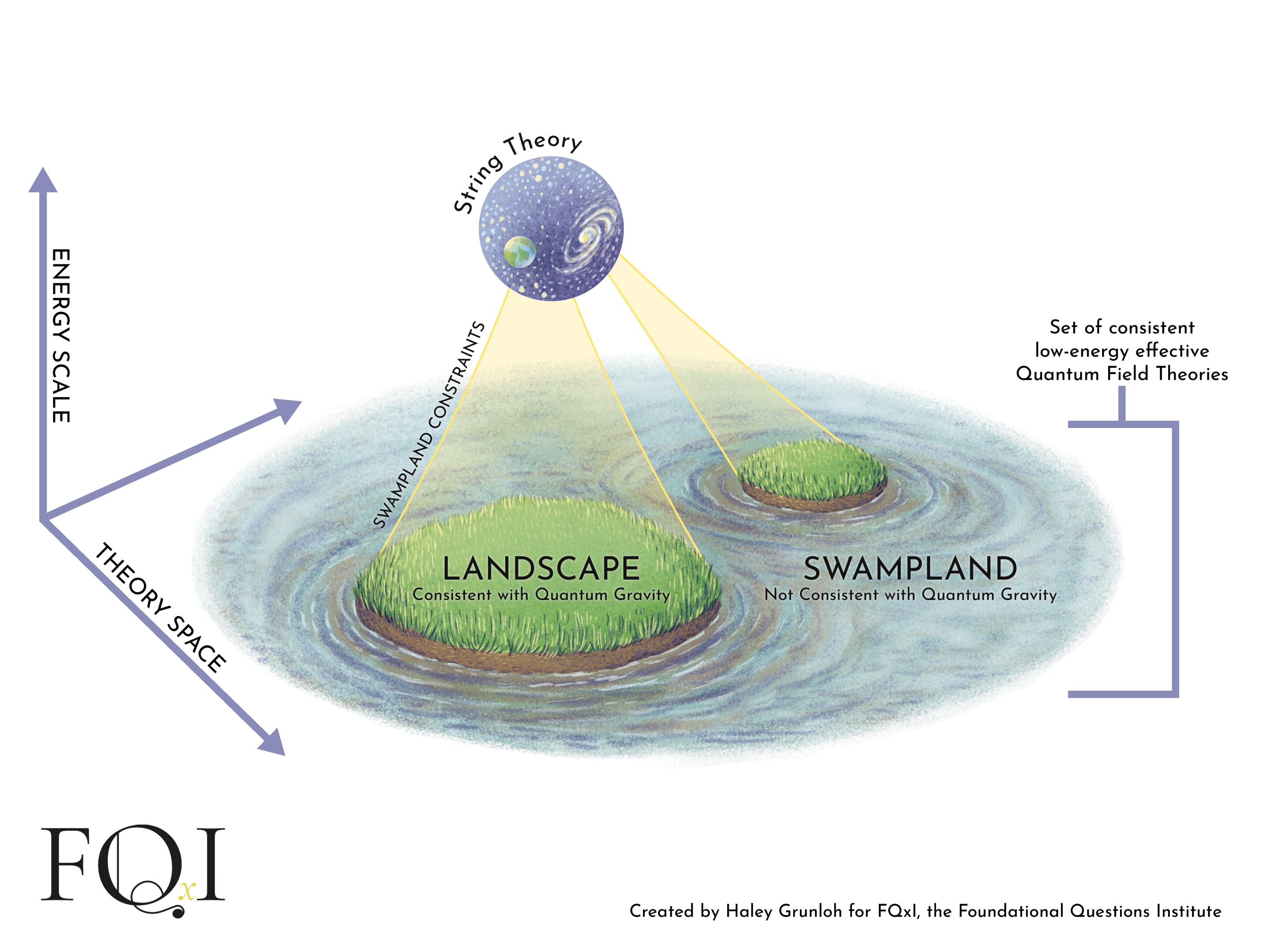
Les équations de la théorie des cordes donnent naissance à une variété quasi infinie d'univers potentiels dans un 'paysage'. Ce paysage est entouré d'un 'marais' de solutions incompatibles avec toute théorie viable de la gravité quantique.
Crédit: Créé par Haley Grunloh pour le Foundational Questions Institute, FQxI FQxI (2025)
Une nouvelle analyse par Eduardo Guendelman, physicien à l'Université Ben-Gourion du Néguev, en Israël, montre qu'un sous-ensemble exotique de modèles de cordes pourrait offrir une échappatoire à ce marais. Dans ces modèles, la tension des cordes est générée dynamiquement.
Dans les années 2000, les théoriciens des cordes ont réalisé que les équations de la théorie ne décrivent pas un seul univers, mais un nombre vertigineux de 10500 solutions possibles. Chacune de ces solutions correspond à un univers avec ses propres particules et forces, créant ce qu'on appelle le 'paysage' de la théorie des cordes.
En 2005, il a été découvert que ce paysage est entouré d'un 'marais' de solutions qui, bien qu'ayant l'air viables, sont en réalité incompatibles avec toute théorie de gravité quantique fonctionnelle. Pour distinguer le paysage du marais, des 'contraintes de marais' ont été proposées.
Guendelman a publié un article dans The European Physical Journal C montrant qu'un certain sous-ensemble exotique de théories des cordes pourrait mieux décrire notre univers réel. Dans ces modèles, la tension des cordes et l'échelle de Planck deviennent dynamiques, affaiblissant les contraintes du marais.
Qu'est-ce que la théorie des cordes ?
La théorie des cordes est une approche théorique en physique qui tente de décrire les particules élémentaires comme des cordes vibrantes minuscules. Ces cordes peuvent vibrer à différentes fréquences, chaque fréquence correspondant à une particule différente.
Cette théorie vise à unifier les quatre forces fondamentales de la nature: la gravité, l'électromagnétisme, la force nucléaire forte et la force nucléaire faible. Elle promet une description cohérente de l'Univers à la fois à l'échelle quantique et cosmologique.
Cependant, la théorie des cordes nécessite l'existence de dimensions spatiales supplémentaires, au-delà des trois que nous connaissons. Ces dimensions supplémentaires sont compactifiées, c'est-à-dire enroulées sur elles-mêmes à des échelles si petites qu'elles échappent à notre perception directe.
Malgré son élégance mathématique, la théorie des cordes n'a pas encore été confirmée par des preuves expérimentales. Elle reste donc une des pistes les plus prometteuses, mais aussi l'une des plus spéculatives, de la physique théorique.
Pourquoi l'énergie noire pose-t-elle un problème à la théorie des cordes ?
L'énergie noire est une forme d'énergie hypothétique qui expliquerait l'accélération de l'expansion de l'Univers. Son existence est déduite des observations astronomiques, mais sa nature exacte reste un mystère.
Dans le cadre de la théorie des cordes conventionnelle, l'énergie noire pose un problème car elle semble incompatible avec les 'contraintes de marais'. Ces contraintes limitent les types d'univers que la théorie peut décrire de manière cohérente avec la gravité quantique.
Les modèles conventionnels de la théorie des cordes prédisent que l'énergie noire devrait être beaucoup plus faible que ce qui est observé, voire inexistante. Cela place notre Univers dans le 'marais' des solutions théoriquement impossibles.
Les travaux de Guendelman suggèrent que des modèles avec une tension dynamique des cordes pourraient contourner ce problème. En rendant l'échelle de Planck dynamique, ces modèles affaiblissent les contraintes et ouvrent la voie à une description cohérente de l'énergie noire.