Sous-ensemble - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
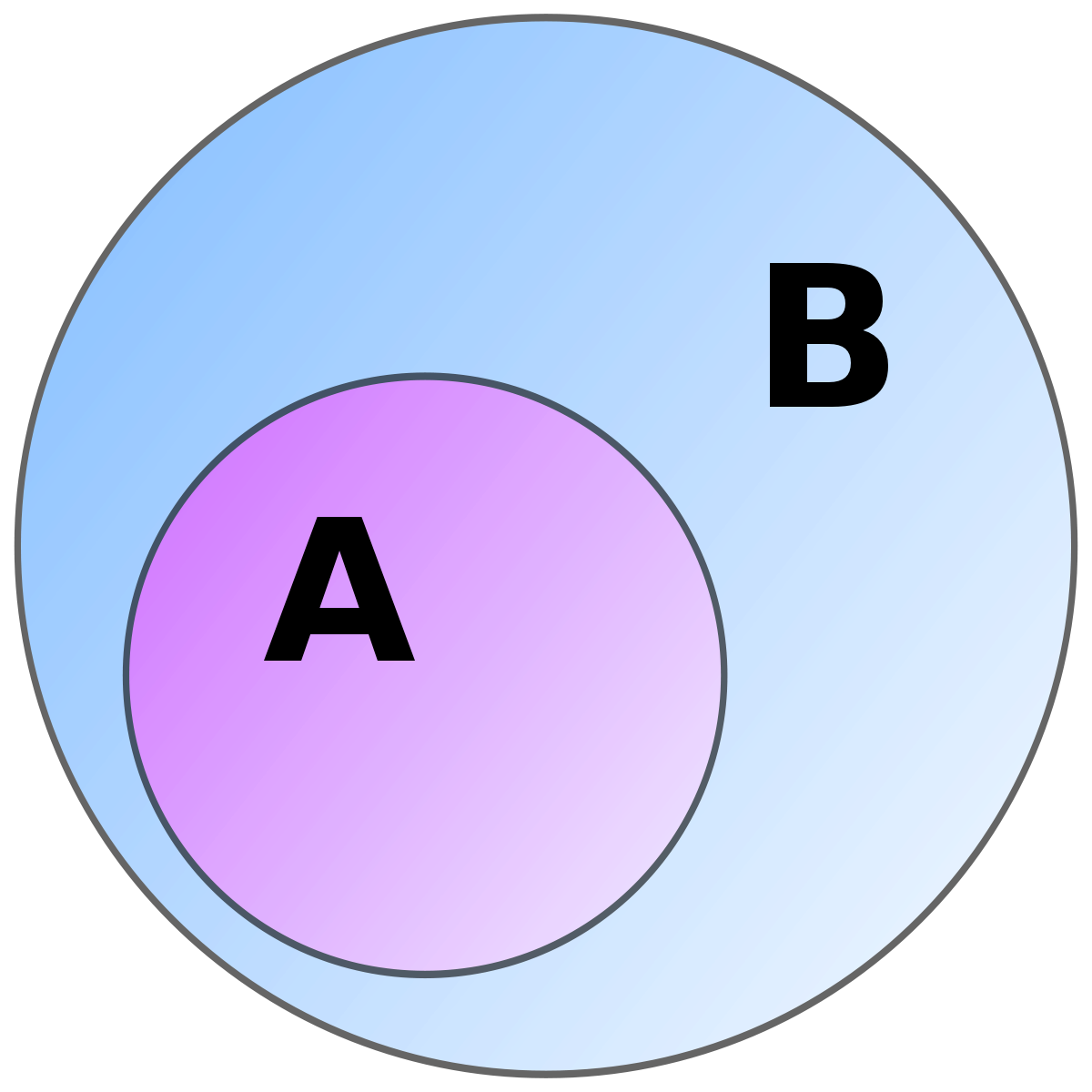
En mathématiques, un ensemble A est un sous-ensemble ou une partie d’un ensemble B, ou encore B est sur-ensemble de A, si tout élément du sous-ensemble A est aussi élément du sur-ensemble B. Il peut par contre y avoir des éléments de B qui ne sont pas éléments de A (voir le diagramme à droite). La relation entre A et B s'appelle l'inclusion.
Définitions
Inclusion, sous-ensembles et sur-ensembles
Soient deux ensembles A et B. Par définition, A est inclus dans B si tout élément de A est un élément de B. En notation symbolique, l’inclusion est notée le plus souvent « ⊂ ». On a alors par définition (« ⇒ » désigne l'implication logique) :
- A ⊂ B signifie ∀ x (x ∈ A ⇒ x ∈ B) .
Par conséquent l'ensemble A n'est pas inclus dans l'ensemble B si et seulement s'il existe un élément de A qui n'appartient pas à B :
- A ⊄ B si et seulement si ∃ x (x ∈ A et x ∉ B) .
Par exemple l'ensemble des entiers naturels non nuls N* est inclus dans l'ensemble des entiers naturels N, de même que l'ensemble des entiers naturels pairs 2N, mais 2N n'est pas inclus dans N* car 0 ∈ 2N, mais 0 ∉ N* :
- N* ⊂ N, 2N ⊂ N, 2N ⊄ N*.
On peut remarquer que, comme il existe des entiers naturels non nuls qui ne sont pas pairs, 1 par exemple, N* n'est pas non plus inclus dans 2N : N* ⊄ 2N. On dit alors que ces deux ensembles ne sont pas comparables pour l'inclusion.
L'inclusion peut se dire de plusieurs façons, « A ⊂ B » peut aussi se lire :
- « A est contenu dans B »,
- « A est une partie de B »,
- ou « A est un sous-ensemble de B ».
et peut aussi s'écrire « B ⊃ A », qui se lit :
- « B inclut A »,
- « B contient A »,
- « B est une extension de A »,
- ou « B est un sur-ensemble de A ».
Il faut prendre garde cependant à l'usage du terme « contient » qui est ambigu, il peut parfois se référer à l'appartenance : A contient x peut parfois signifier que A ∋ x (c'est-à-dire x ∈ A).
Définition en compréhension
Une propriété des éléments d'un ensemble définit un sous-ensemble de celui-ci. Ainsi, en reprenant l'un des exemples ci-dessus, la propriété « être pair » définit, sur l'ensemble des entiers naturels N, l'ensemble 2N des entiers pairs. On dit que l'ensemble a été défini par compréhension et on note :
- 2N={n ∈ N | n est pair} = {n ∈ N | (∃q ∈ N) n=2q}
Toute propriété (quand on l'exprime dans un langage précis on parle de prédicat de ce langage) définit par compréhension un sous-ensemble d'un ensemble donné.
Inclusion stricte et sous-ensembles propres
Remarquons qu'un ensemble est toujours sous-ensemble de lui-même (voir proposition 2 ci-dessous). Il peut être nécessaire d'exclure ce cas et de ne considérer que des sous-ensembles différents de l'ensemble lui-même. C'est pourquoi on définit une inclusion stricte, notée « ⊊ » . Un ensemble A est strictement inclus dans un ensemble B si et seulement si A est inclus dans B sans lui être égal :
-
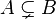
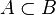
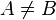
L'inclusion habituelle peut alors être qualifiée d’inclusion large, s'il y a risque d'ambiguïté.
À part lui-même, un ensemble compte toujours au moins un autre sous-ensemble : l'ensemble vide. Ces deux sous-ensembles sont parfois dits « triviaux ».
Une partie de A distincte de A lui-même est appelée un sous-ensemble propre de A.
Ainsi, en reprenant l'exemple du paragraphe précédent, l'ensemble des entiers naturels pairs 2N, comme l'ensemble des entiers naturels non nuls N*, sont des sous-ensembles propres de l'ensemble des entiers naturels N.
Ensemble des parties
L'ensemble de tous les sous-ensembles d'un ensemble E donné est appelé ensemble des parties de E, et noté habituellement «
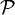
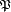
On a ainsi :
- X ∈
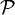
Par exemple si A = { a, b }, alors
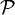
Dans ce cas on aura par exemple a ∈ A, donc {a} ⊂ A, c'est-à-dire {a} ∈
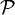
Les propriétés de l'ensemble des parties, en particulier celles ayant trait à la cardinalité, sont détaillées dans l'article ensemble des parties d'un ensemble. Pour le cas fini, qui relève de la combinatoire, voir aussi l'article combinaison.
Fonction caractéristique
Un sous-ensemble A d'un ensemble E peut être défini par sa fonction caractéristique χA
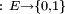
et donc (χA étant à valeurs dans {0,1})
Réciproquement toute fonction χ de E dans {0,1} définit un sous-ensemble de E qui est {x ∈ E | χ(x)=1}. On a donc une correspondance bijective entre les sous-ensembles de E et les fonctions de E dans {0,1}, c'est-à-dire entre
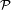
![\forall x \in E[ \chi_A(x) = 1 \Leftrightarrow x \in A ]](https://static.techno-science.net/illustration/Definitions/autres/9/94ec4baa03260c91ffc084d6dbe27b7a_6d2f2d29ebcc6e38e1bb32b53bc11261.png)
![\forall x \in E[\chi_A( x) = 0 \Leftrightarrow x \not\in A ]](https://static.techno-science.net/illustration/Definitions/autres/8/85e314907b883a8bc32d002aae4a78ba_a4fbf79f37db5a512c1c4a15d4ab58fe.png)

















































