Cosmologie: l'Espace Dodécaédrique de Poincaré
Restez toujours informé: suivez-nous sur Google Actualités (icone ☆)

Figure 1-A: L'espace dodécaédrique de Poincaré peut se décrire comme l'intérieur
d'un dodécaèdre sphérique tel que, si l'on "sort" par une face pentagonale,
on "rentre" immédiatement par la face opposée après une rotation de 36°.
Un tel espace est donc fini, bien que sans frontière ni bord,
de sorte que l'on peut y voyager indéfiniment sans obstacle
Les quinze dernières années ont vu un accroissement considérable des efforts pour déterminer la forme globale de l'univers, c'est-à-dire non seulement la courbure de l'espace mais aussi sa topologie. Le modèle cosmologique dit de "concordance" qui prévaut actuellement décrit l'univers par un espace "plat" (c'est-à-dire de courbure nulle), infini, en expansion perpétuelle accélérée. Cependant, les données délivrées entre 2003 et 2006 par le satellite WMAP de la NASA, qui ont fourni une carte à haute résolution du rayonnement de fond cosmologique (CMB), s'accordent très mal avec le modèle de concordance aux grandes échelles angulaires. Elles favorisent plutôt un espace fini, de courbure positive, et suggèrent une topologie multi-connexe.

Figure 1-B: Vue depuis l'intérieur de PDS perpendiculairement à une face pentagonale.
L'observateur a l'illusion de vivre dans un espace 120 fois plus grand,
construit comme une mosaïque de dodécaèdres empilés dont les images
se répètent comme dans une galerie des glaces
Le CMB est le vestige de la première lumière émise peu après le Big Bang. Il est observé sur la "surface de dernière diffusion" (LSS), une sphère d'environ 50 milliards d'années-lumière de rayon qui nous entoure. Les minuscules fluctuations de température observées sur la LSS peuvent être décomposées en une somme d'harmoniques sphériques, tout comme le son produit par un instrument de musique peut être décomposé en harmoniques ordinaires. Les amplitudes relatives de chaque harmonique sphérique détermine le spectre de puissance, qui est une signature de la géométrie de l'espace et des conditions physiques qui régnaient à l'époque d'émission du CMB.
Or, la topologie cosmique prédit que tout espace physique qui serait plus petit que la LSS ne pourrait vibrer sur des longueurs d'onde plus grandes que sa propre taille. Il devrait en résulter une coupure de son spectre de puissance au-dessus d'une certaine longueur d'onde. Cette coupure aux grandes échelles a précisément été observée par la campagne d'observations 2003-2006 du télescope WMAP.
Se fondant sur la possibilité que l'espace ait une courbure positive, et en calculant certains modes vibrationnels de l'espace pour simuler le spectre de puissance, certains auteurs de la présente étude avaient déjà proposé en octobre 2003 que la topologie multi-connexe de l'espace dodécaédrique de Poincaré (PDS, figures 1-A, 1-B et 1-C) était favorisée par les données de WMAP, au détriment de l'espace simplement connexe, plat et infini stipulé par le modèle de concordance.
Le modèle PDS a depuis lors été étudié mathématiquement en grand détail par plusieurs groupes à travers le monde. Dans l'étude la plus récente, Jean-Pierre Luminet (Observatoire de Paris, LUTH et CNRS) et ses collaborateurs ont calculé 1,7 milliards de modes vibrationnels de PDS pour simuler avec plus de précision qu'en 2003 le spectre de puissance, sur une large gamme d'échelles angulaires. Ils ont trouvé que la diminution maximale de l'harmonique quadripolaire, telle qu'elle apparaît dans les données, requiert une densité de matière-énergie optimale de Ωtot = 1,018 (voir note en bas de l'article). Le spectre de puissance ainsi prédit par le modèle PDS s'accorde remarquablement avec la totalité du spectre WMAP observé (figure 2).
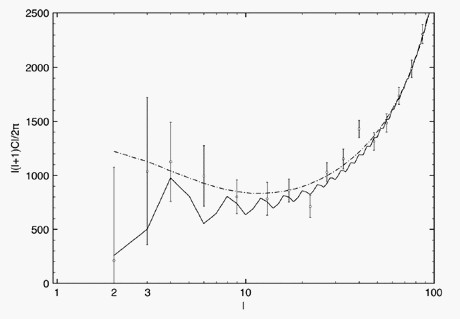
Figure 2: Spectres de puissance comparés
pour les données expérimentales de WMAP (barres d'erreur verticales),
pour le modèle théorique de concordance tel que
Ωtot = 1,000, Ωmat = 0,27 et h = 0,70 (courbe en pointillés)
et pour le modèle PDS tel que Ωtot = 1,018 (courbe pleine)
Une signature par les cercles
Si l'espace physique est plus petit que l'espace observé contenu dans la sphère LSS, il doit y avoir des corrélations particulières dans le CMB, à savoir des paires de cercles "homologues" le long desquels les fluctuations de température sont les mêmes, car ils correspondent aux mêmes points physiques observés dans des directions différentes, suite à un effet de mirage topologique. La signature précise et définitive de la topologie PDS serait l'existence de six paires de cercles diamétralement opposés, corrélés avec une phase relative de 36°. Pour tester cette prédiction, l'équipe de chercheurs a simulé des cartes du CMB dans la topologie PDS et vérifié la présence des cercles corrélés (figure 3).

Figure 3: Simulation de la surface de dernière diffusion
et de ses plus proches copies dans la topologie PDS.
Comme le volume de l'espace PDS ne représente que 80% du volume de la sphère LSS,
celle-ci s'auto-intersecte selon six paires antipodales de cercles homologues,
qui représentent les mêmes points de l'espace à une rotation de 36° près
Reste la question cruciale: ces paires de cercles corrélés sont-elles présentes dans les données réelles de WMAP ? Trois équipes différentes (américaine, allemande et polonaise) se sont penchées sur le problème au cours des cinq dernières années, en utilisant divers indicateurs statistiques et des simulations numériques massives. Aucune réponse claire n'émerge pour l'instant de ces travaux, car le signal topologique attendu est dégradé par divers effets cosmologiques, ainsi que par les contaminations de fond astrophysiques et les imperfections instrumentales, qui tous induisent du bruit.
C'est pourquoi une autre équipe internationale de cosmologistes conduite par B. Roukema de l'Université de Torun en Pologne (précédemment chercheur à l'Observatoire de Paris), a réanalysé les données WMAP à l'aide de nouvelles méthodes statistiques. Ils ont montré que les corrélations croisées entre les fluctuations de température évaluées sur les éventuelles copies multiples de la LSS entraînent une forte corrélation en faveur d'une symétrie dodécaédrique dans la carte WMAP, ainsi qu'une phase relative de 36° pour les paires de cercles homologues. En déterminant la position de ces cercles, ils ont même pu fixer l'orientation spatiale du dodécaèdre fondamental par rapport à la carte WMAP (figure 4).
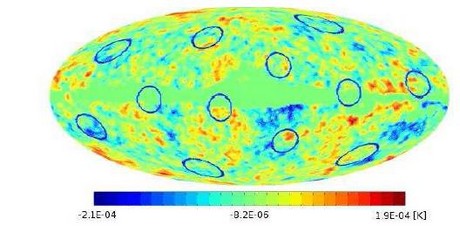
Figure 4: Position des 12 cercles corrélés trouvés récemment dans les données WMAP
par une équipe franco-polonaise, en parfait accord avec le modèle PDS.
Les centres des cercles correspondent aux centres des faces du dodécaèdre fondamental, déterminés par leurs coordonnées galactiques.
La probabilité pour que le modèle de concordance plat et infini reproduise par hasard
une telle configuration n'est que 7%
Conclusion
Vivons-nous réellement dans un espace dodécaédrique de Poincaré ? Des contraintes expérimentales futures pour ou contre le modèle seront certainement nécessaires, mais les indices en faveur d'un signal topologique PDS dans les données WMAP s'accumulent. Pour faire avancer le débat, les futures données du satellite européen Planck Surveyor (lancement prévu en juillet 2008) sont attendues avec impatience.
Note
Le paramètre de densité Ωtot caractérise le contenu de l'univers, toutes formes de matière et d'énergie confondues. La courbure de l'espace dépend de la valeur de ce paramètre. Si Ωtot est plus grand que 1, la courbure de l'espace est positive et la géométrie est de type sphérique ; si Ωtot est plus petit que 1, la courbure est négative et la géométrie est hyperbolique; ce n'est que si Ωtot est strictement égal à 1 que l'espace est Euclidien.
