Follow us on Google News (click on ☆)

In almost all human cultures, music is based on pitch scales. These scales define, for creating melodies and harmonies, a small number of admissible frequency ratios between two notes, among an infinite number of possibilities. Many scales use the simple ratios 2:1, 3:2, and 4:3, corresponding to intervals called "octave," "fifth," and "fourth" in Western music.
Why are these ratios so common?
The presence of simple ratios in musical scales is generally explained by the fact that they favor the consonance of simultaneous notes, due to physical and sensory phenomena. For successive notes, however, the dominant opinion is that there is no interval more "natural" than another.
Certainly, a melody based on a scale including the octave, fifth, and fourth will often be perceived by a Western listener as "more harmonious" than another. But this preference is often attributed to an acculturation phenomenon, where we tend to prefer what is familiar to us, and we are all, musicians or not, accustomed to scales with simple ratios.
The study published in Current Biology suggests that, contrary to the dominant opinion, the octave, fifth, and fourth are indeed natural melodic intervals, made perceptually special by the functioning of the auditory system of every human being, regardless of their culture.
The scientists' demonstration involved training young Western adults to detect anomalies ("wrong notes") in random melodies of pure tones, based on various musical scales. Some of these scales were specially designed for this study. The experiment required no prior musical knowledge. The training was lengthy, to achieve saturation of familiarity with the scales.
The main result shows that the subjects performed better with scales containing simple frequency ratios (2:1, 3:2, and 4:3), not only at the beginning of the training—which could a priori be interpreted as a familiarity effect (acculturation)—but also at the end of the training, which had compensated for any initial lack of familiarity disadvantage. A computational model suggests that these simple ratios are better represented in memory, which could explain the behavioral results.
The study thus suggests that the use of frequency ratios in musical scales is largely dictated by our natural perception of melodies, contrary to the hypothesis that melody perception is culturally shaped by musical scales, which are thus a determinant rather than a consequence.
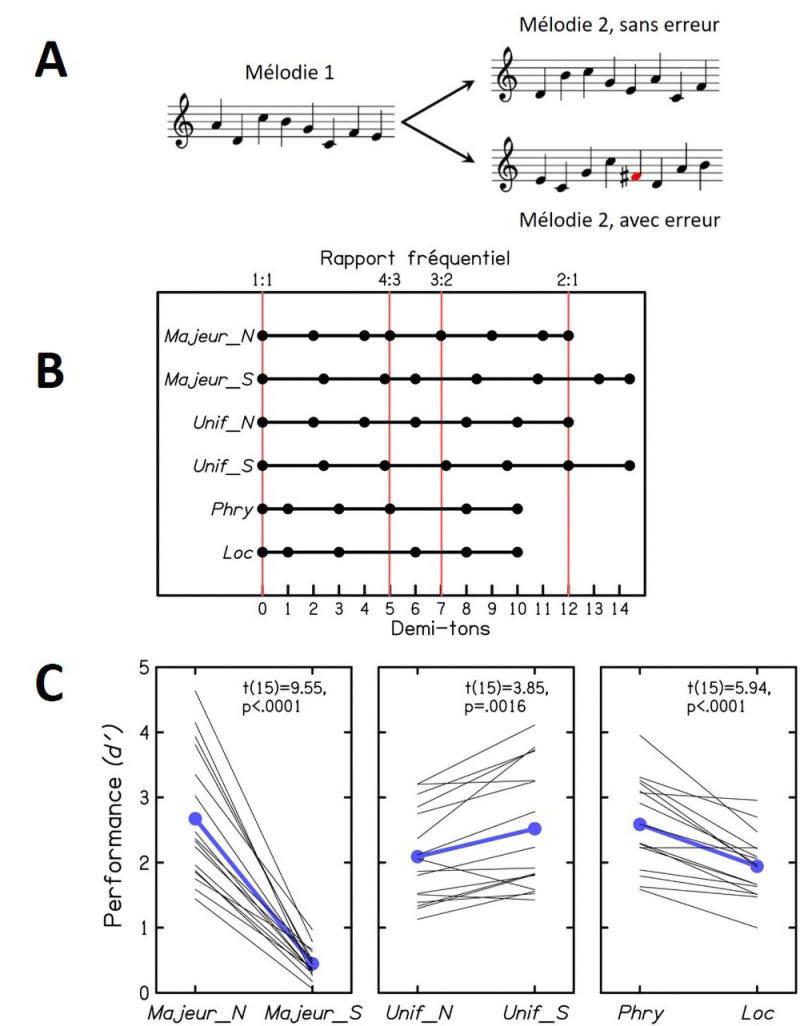
A. Illustration of the experimental task. For each "trial," two melodies were presented. Melody 1 was formed from all the notes of a certain musical scale, randomly ordered, also randomly choosing the frequency register of the melody; in the depicted example, the scale is "Major_N," the normal diatonic major scale. Melody 2 randomly reordered the sounds of Melody 1, either without any error or with a half-tone error violating the scale of Melody 1. The subject had to indicate whether Melody 2 contained a sound absent from Melody 1 or not.
B. Six scales used in the study. Major_S is obtained by stretching Major_N by 20%; this stretching eliminates the simple frequency ratios 2:1 and 3:2, present (almost exactly) in Major_N. Unif_N, a scale dear to Debussy, divides the octave (2:1) into six equal intervals and contains no simple frequency ratio other than 2:1. Unif_S stretches Unif_N by 20%; this stretching preserves the 2:1 ratio and also produces ratios close to 3:2 and 4:3. Phry and Loc derive from the so-called "Phrygian" and "Locrian" diatonic scales; they differ from each other only by their fourth degree, forming a simple ratio (4:3) with the first degree only in the case of Phry.
C. "Final" performances obtained for the six scales depicted in B. Each thin line represents a subject; in blue, the average results. The left panel shows that the transformation from Major_N to Major_S strongly degraded performance. The central panel shows that the same transformation (a 20% stretch) improved performance from Unif_N to Unif_S. The right panel indicates that performance was better for Phry than for Loc. Overall, these results show that performance was facilitated by the presence of simple frequency ratios (at least approximately) in the musical scale of Melody 1.
© Laurent Demany, Catherine Semal, & Daniel Pressnitzer
Learn more: Demany L, Semal C, Pressnitzer D. Simple frequency ratios naturally make precisely perceived melodies. Curr Biol. 2025 Mar 6:S0960-9822(25)00193-9. doi: 10.1016/j.cub.2025.02.030. Epub ahead of print. PMID: 40081379.