
Em quase todas as culturas humanas, a música se baseia em escalas de altura tonal. Essas escalas definem, para criar melodias e harmonias, um pequeno número de relações de frequência admissíveis entre duas notas, entre uma infinidade de possibilidades. Muitas escalas usam as relações simples 2:1, 3:2 e 4:3, correspondendo a intervalos chamados de "oitava", "quinta" e "quarta" na música ocidental.
Por que essas relações são tão comuns?
A presença de relações simples nas escalas musicais é geralmente explicada pelo fato de que elas favorecem a consonância de notas simultâneas, devido a fenômenos físicos e sensoriais. Para notas sucessivas, por outro lado, a opinião dominante é que não há um intervalo mais "natural" do que outro.
Certamente, uma melodia baseada em uma escala que inclui a oitava, a quinta e a quarta será frequentemente percebida por um ouvinte ocidental como "mais harmoniosa" do que outra. Mas essa preferência é frequentemente atribuída a um fenômeno de aculturação, onde tendemos a preferir o que nos é familiar e todos nós, músicos ou não, estamos acostumados com escalas que contêm relações simples.
O estudo publicado na Current Biology sugere que, ao contrário da opinião dominante, a oitava, a quinta e a quarta são de fato intervalos melódicos naturais, tornados perceptivelmente especiais pelo funcionamento do sistema auditivo de qualquer ser humano, independentemente de sua cultura.
A demonstração dos cientistas consistiu em treinar jovens adultos ocidentais a detectar anomalias ("notas falsas") em melodias aleatórias de sons puros, baseadas em várias escalas musicais. Algumas dessas escalas foram especialmente projetadas para este estudo. O experimento não exigia nenhum conhecimento musical prévio. O treinamento foi longo, de modo a alcançar uma saturação da familiaridade com as escalas.
O principal resultado mostra que os participantes tiveram melhor desempenho com as escalas que incluíam relações de frequência simples (2:1, 3:2 e 4:3), não apenas no início do treinamento - o que poderia a priori ser interpretado como um efeito de familiaridade (aculturação) - mas também no final do treinamento, que havia compensado a possível desvantagem de uma falta inicial de familiaridade. Um modelo computacional sugere que essas relações simples são melhor representadas na memória, o que poderia explicar os resultados comportamentais.
O estudo sugere, portanto, que o uso de relações de frequência nas escalas musicais é em grande parte ditado por nossa percepção natural das melodias, em oposição à hipótese de que a percepção das melodias é moldada culturalmente por escalas musicais que são, assim, um determinante em vez de uma consequência.
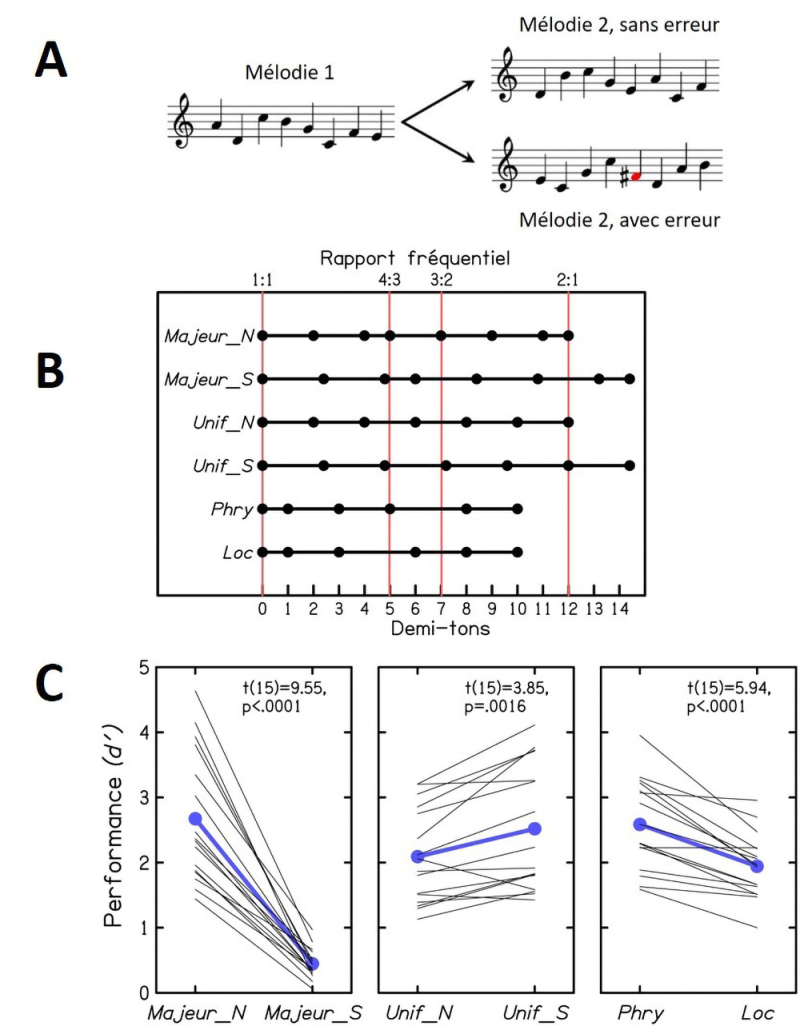
A. Ilustração da tarefa experimental. Em cada "tentativa", duas melodias eram apresentadas. A melodia 1 era formada por todas as notas de uma determinada escala musical, ordenadas aleatoriamente, escolhendo também aleatoriamente o registro de frequência da melodia; no exemplo mostrado, a escala é "Maior_N", a escala diatônica maior normal. A melodia 2 reordenava aleatoriamente os sons da melodia 1, seja sem nenhum erro ou com um erro de meio tom violando a escala da melodia 1. O participante deveria indicar se a melodia 2 continha ou não um som ausente da melodia 1.
B. Seis escalas usadas no estudo. Maior_S é obtida esticando Maior_N em 20%; esse estiramento elimina as relações de frequência simples 2:1 e 3:2, presentes (quase exatamente) em Maior_N. Unif_N, escala cara a Debussy, divide a oitava (2:1) em seis intervalos iguais e não contém nenhuma relação de frequência simples além de 2:1. Unif_S estica Unif_N em 20%; esse estiramento preserva a relação 2:1 e também produz relações próximas de 3:2 e 4:3. Phry e Loc derivam das escalas diatônicas chamadas "Frígia" e "Lócria"; elas diferem uma da outra apenas pelo seu quarto grau, formando uma relação simples (4:3) com o primeiro grau apenas no caso de Phry.
C. Desempenhos "finais" obtidos para as seis escalas mostradas em B. Cada linha fina representa um participante; em azul, os resultados médios. Vê-se no painel esquerdo que a transformação de Maior_N em Maior_S degradou fortemente os desempenhos. O painel central mostra que a mesma transformação (um estiramento de 20%) melhorou, por outro lado, os desempenhos de Unif_N para Unif_S. O painel da direita indica que os desempenhos foram melhores para Phry do que para Loc. Conclui-se desses resultados que o desempenho foi facilitado pela presença de relações de frequência simples (pelo menos aproximadamente) na escala musical da melodia 1.
© Laurent Demany, Catherine Semal, & Daniel Pressnitzer
Saiba mais: Demany L, Semal C, Pressnitzer D. Simple frequency ratios naturally make precisely perceived melodies. Curr Biol. 2025 Mar 6:S0960-9822(25)00193-9. doi: 10.1016/j.cub.2025.02.030. Epub ahead of print. PMID: 40081379.