
En casi todas las culturas humanas, la música se basa en escalas de altura tonal. Estas escalas definen, para crear melodías y armonías, un pequeño número de relaciones de frecuencia admisibles entre dos notas, entre una infinidad de posibilidades. Muchas escalas utilizan las relaciones simples 2:1, 3:2 y 4:3, correspondientes a intervalos llamados "octava", "quinta" y "cuarta" en la música occidental.
¿Por qué son tan comunes estas relaciones?
La presencia de relaciones simples en las escalas musicales generalmente se explica por el hecho de que favorecen la consonancia de notas simultáneas, debido a fenómenos físicos y sensoriales. Para notas sucesivas, en cambio, la opinión dominante es que no hay un intervalo más "natural" que otro.
Ciertamente, una melodía basada en una escala que incluye la octava, la quinta y la cuarta a menudo será percibida por un oyente occidental como "más armoniosa" que otra. Pero esta preferencia suele atribuirse a un fenómeno de aculturación, donde tendemos a preferir lo que nos es familiar y todos, músicos o no, estamos acostumbrados a escalas con relaciones simples.
El estudio publicado en Current Biology sugiere que, contrariamente a la opinión dominante, la octava, la quinta y la cuarta son efectivamente intervalos melódicos naturales, hechos perceptivamente especiales por el funcionamiento del sistema auditivo de todo ser humano, independientemente de su cultura.
La demostración de los científicos consistió en entrenar a jóvenes adultos occidentales para detectar anomalías ("notas falsas") en melodías aleatorias de sonidos puros, basadas en diversas escalas musicales. Algunas de estas escalas fueron diseñadas especialmente para este estudio. El experimento no requería ningún conocimiento musical previo. El entrenamiento fue largo, para lograr una saturación de la familiaridad con las escalas.
El principal resultado muestra que los sujetos tuvieron mejor desempeño con las escalas que incluían relaciones frecuenciales simples (2:1, 3:2 y 4:3), no solo al inicio del entrenamiento - lo que a priori podría interpretarse como un efecto de familiaridad (aculturación) - sino también al final del entrenamiento, que había compensado la posible desventaja de una falta inicial de familiaridad. Un modelo computacional sugiere que estas relaciones simples están mejor representadas en la memoria, lo que podría explicar los resultados conductuales.
El estudio sugiere, por tanto, que el uso de relaciones frecuenciales en las escalas musicales está en gran parte dictado por nuestra percepción natural de las melodías, en contraposición a la hipótesis de que la percepción de las melodías está moldeada culturalmente por escalas musicales que son así un determinante más que una consecuencia.
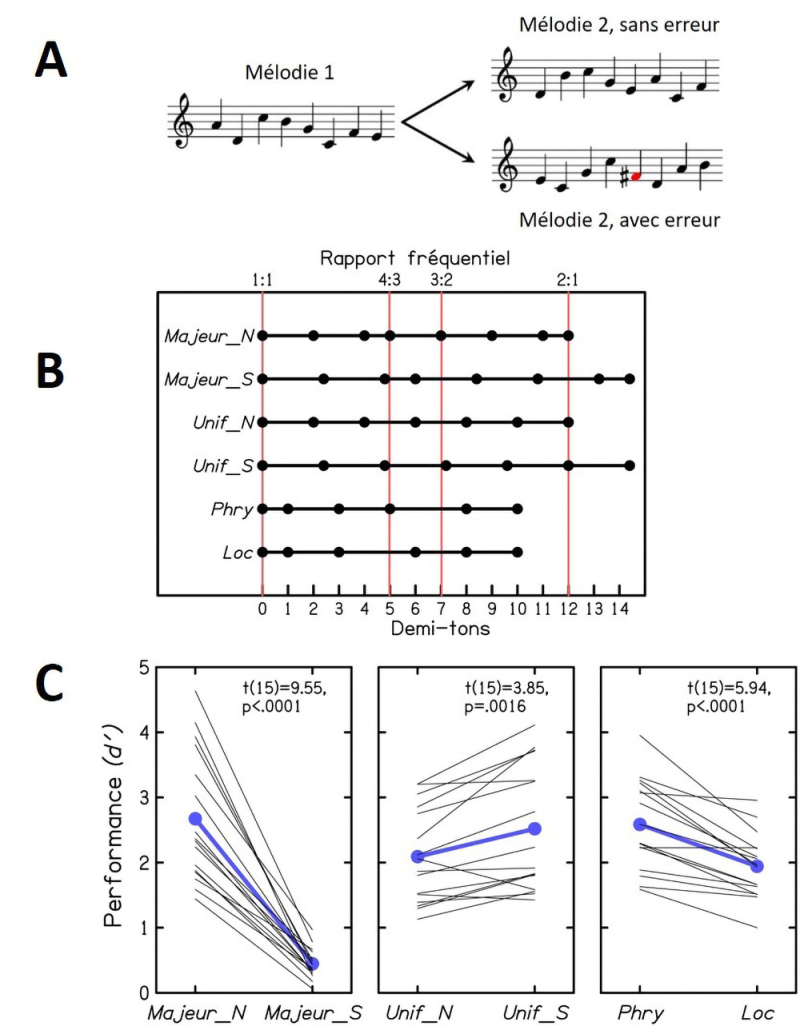
A. Ilustración de la tarea experimental. En cada "ensayo", se presentaban dos melodías. La melodía 1 estaba formada por todas las notas de una cierta escala musical, ordenadas al azar, eligiendo también al azar el registro frecuencial de la melodía; en el ejemplo mostrado, la escala es "Mayor_N", la escala diatónica mayor normal. La melodía 2 reordenaba al azar los sonidos de la melodía 1, ya sea sin ningún error o con un error de un semitono que violaba la escala de la melodía 1. El sujeto debía indicar si la melodía 2 contenía o no un sonido ausente en la melodía 1.
B. Seis escalas utilizadas en el estudio. Mayor_S se obtiene estirando Mayor_N un 20%; este estiramiento elimina las relaciones frecuenciales simples 2:1 y 3:2, presentes (casi exactamente) en Mayor_N. Unif_N, escala apreciada por Debussy, divide la octava (2:1) en seis intervalos iguales y no contiene ninguna relación frecuencial simple aparte de 2:1. Unif_S estira Unif_N un 20%; este estiramiento preserva la relación 2:1, y también produce relaciones cercanas a 3:2 y 4:3. Phry y Loc derivan de las escalas diatónicas llamadas "Frigia" y "Locria"; solo difieren entre sí por su cuarto grado, formando una relación simple (4:3) con el primer grado solo en el caso de Phry.
C. Desempeños "finales" obtenidos para las seis escalas mostradas en B. Cada línea fina representa un sujeto; en azul los resultados promedios. Se ve en el panel izquierdo que la transformación de Mayor_N en Mayor_S degradó fuertemente los desempeños. El panel central muestra que la misma transformación (un estiramiento del 20%) mejoró, en cambio, los desempeños de Unif_N a Unif_S. El panel de la derecha indica que los desempeños fueron mejores para Phry que para Loc. Se desprende de estos resultados que el desempeño fue facilitado por la presencia de relaciones frecuenciales simples (al menos aproximadamente) en la escala musical de la melodía 1.
© Laurent Demany, Catherine Semal, & Daniel Pressnitzer
Saber más: Demany L, Semal C, Pressnitzer D. Simple frequency ratios naturally make precisely perceived melodies. Curr Biol. 2025 Mar 6:S0960-9822(25)00193-9. doi: 10.1016/j.cub.2025.02.030. Epub ahead of print. PMID: 40081379.