Nombre irrationnel - Définition

Introduction

Un nombre irrationnel est un nombre réel qui n'est pas rationnel, c'est-à-dire qu'il ne peut pas s'écrire sous la forme d'une fraction , où a et b sont deux entiers relatifs (avec b non nul).

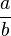
Les premiers nombres irrationnels découverts sont les racines carrées des entiers qui ne sont pas des carrés parfaits, entre autres (voir la démonstration d'irrationalité). Plus généralement, on appelle nombres algébriques les nombres qui sont racine d'un polynôme à coefficients rationnels ; cette catégorie facile à construire permet d'exhiber de nombreux nombres irrationnels. Les nombres qui ne sont pas algébriques (c'est-à-dire qui ne sont racine d'aucun polynôme à coefficients rationnels) sont appelés nombres transcendants ; ils sont tous irrationnels. π (pi) et e font partie de cette seconde catégorie de nombres irrationnels.

Histoire

Comme le rapporte le Sulba Sutras, l'utilisation la plus ancienne des nombres irrationnels fut faite par les indiens entre 800 et 500 avant J-C. Il était connu que la diagonale et l'un des côtés d'un carré sont incommensurables l'une à l'autre.

Contrairement à une idée reçue, rien n'indique avec certitude que la découverte de l'incommensurabilité provienne de l'étude de la diagonale et de l'un des côtés d'un carré, propriété équivalente à l'irrationnalité de √2. La découverte est parfois attribuée au mathématicien Hippase de Métaponte pour ces travaux sur la section d'extrême et de moyenne raison, maintenant appelée nombre d'or. Elle reste encore l'objet d'un profond mystère. On admet généralement qu'elle est l'oeuvre d'un Pythagoricien durant la première moitié du V^e siècle avant J-C . Cette découverte ouvrit probablement une crise profonde chez les mathématiciens et les philosophes grecs. Une légende, plusieurs fois rapportée, indique qu'un pythagoricien, parfois nommé Hippase, périt noyé pour avoir révélé aux profanes l'incommensurabilité. Cette légende indiquerait que la découverte est bien pythagoricienne et qu'elle faisait l'objet d'un tabou.

La première démonstration date d'avant -410 et porte probablement sur l'étude de √2. Plusieurs idées de démonstration sont imaginées, l'une d'elle repose sur le principe du pair et de l'impair. Ce principe remontant au début du V^e siècle, la démonstration pourrait être ancienne. D'autres démonstrations sont imaginées, à l'aide d'une descente infinie ou encore d'un algorithme qu'en termes modernes on apparenterait aux fractions continues et dont une forme ancienne est héritée des mésopotamiens. Le livre X des éléments d'Euclide est consacré à une classification des grandeurs irrationnelles.

Au XVI^e siècle, la communauté mathématique accueillit favorablement les nombres négatifs et les fractions. Au XVII^e siècle, les mathématiciens employèrent de plus en plus fréquemment les fractions décimales et représentaient déjà ces nombres avec la notation moderne.

Pendant les cent années suivantes furent introduits les nombres imaginaires qui devinrent un outil puissant forgé par Abraham de Moivre, et plus particulièrement aiguisé par Leonhard Euler.

Au dix-neuvième siècle, la théorie des nombres complexes fut complétée, l'existence des nombres transcendants fut montrée, ce qui amena à diviser les nombres irrationnels en deux catégories, celle des nombres algébriques et celle des nombres transcendants et ainsi à effectuer une étude scientifique d'un sujet presque resté en léthargie depuis Euclide, celui de la théorie des nombres irrationnels.

L'année 1872, vit la publication des théories de Karl Weierstrass (par son élève Kossak), de Heine (Crelle 74), de George Cantor (Annalen 5), et de Richard Dedekind. Méray avait pris en 1869 les mêmes points de départ que Heine, mais la naissance de cette théorie est généralement rattachée à l'année 1872.

La méthode de Weierstrass fut complètement déterminée par Pincherle (en 1880), et celle de Dedekind reçut une importance supplémentaire par le travail ultérieur de l'auteur (en 1888) et par l'approbation plus récente de tannerie de Paul (en 1894).

Weierstrass, Cantor, et Heine basèrent leurs théories sur les séries infinies, pendant que Dedekind fonda la sienne sur l'idée d'une coupure (Schnitt) dans le système des nombres rationnels, partageant les nombres rationnels en deux classes caractérisées par des propriétés différentes.

Ce travail fut complété plus tard par Weierstrass, Kronecker (Crelle 101), et Méray.

Les fractions continues, étroitement liées aux nombres irrationnels (dues à Cataldi en 1613), furent prises en considération par Euler, et au début du dix-neuvième siècle, elles prirent de l'importance grâce aux écrits de Joseph Louis Lagrange. Dirichlet aussi travailla sur cette théorie, ainsi que beaucoup d'autres mathématiciens qui développèrent de multiples applications.

Lambert démontra en 1761 que π ne pouvait être rationnel, et que eⁿ est irrationnel si n est rationnel (sauf si n = 0).

La démonstration de l'irrationalité de π de Lambert, est considérée comme incomplète selon les critères actuels. Mais les historiens des mathématiques l'acceptent satisfaisante et la jugent rigoureuse pour son époque. La méthode consiste à approcher π par des rationnels, les propriétés de cette suite de nombres montrent que la limite est nécessairement irrationnelle.

Legendre (en 1794), après avoir introduit les fonctions de Bessel-Clifford, fournit une démonstration de l'irrationalité de π² confirmant ainsi celle de π.

L'existence de nombres transcendants a été établie pour la première fois par Liouville (entre 1844 et 1851). En 1873, George Cantor montra leur existence par une méthode différente, en démontrant que tout intervalle ayant au moins deux réels contient des nombres transcendants. Charles Hermite (en 1873) fut le premier à démontrer la transcendance de e, et Ferdinand von Lindemann (en 1882), montra à partir des conclusions d'Hermite, la transcendance de π. La démonstration de Lindemann fut largement simplifiée par Weierstrass (en 1885), et encore davantage par David Hilbert (en 1893), pour finalement devenir élémentaire grâce à Adolf Hurwitz et Paul Albert Gordan.