Lundi 4 Août 2025
Rechercher 🔍
Mathématiques

Fonction digamma - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs est disponible ici.

En mathématiques, la fonction digamma est définie par

où D est l'opérateur différentiel.

La fonction digamma, souvent notée aussi 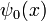\psi_0(x)\, ou même 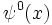\psi^0(x)\, , est reliée aux nombres harmoniques par

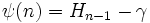
\psi(n) = H_{n-1}-\gamma\,

où 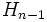H_{n-1}\, est le (n - 1)-ième nombre harmonique, et 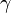\gamma\, est la célèbre constante d'Euler-Mascheroni.

miniature
🔵 Quel est le secret du bleu maya ?
miniature
🚨 L'obésité, un facteur de l'explosion des décès par cancer
miniature
🔭 Notre place dans l'Univers serait particulière, et cela explique bien des choses
miniature
🍉 Pourquoi les fruits d'été sont-ils si sucrés ?
miniature
🔭 Des forces cachées aux confins du Système solaire ?
miniature
🌍 Découverte de structures anciennes cachées sous l'Antarctique, et cela nous concerne directement
miniature
📢 Comment les cigales font-elles leur bruit ?
miniature
🌊 C'est énorme: 27 millions de tonnes de plastiques déversés dans l'Atlantique Nord
miniature
🔭 Cette observation suggère que tout pourrait venir de la ceinture d'astéroïdes
miniature
🦴 Comment les pythons digèrent-ils les os sans laisser de trace ?
miniature
💫 Comment un pulsar milliseconde a trompé les astronomes pendant des années ?
miniature
🌱 Par évolution dirigée, le MIT a fortement amélioré l'efficacité de la photosynthèse
miniature
🌍 Une météorite a-t-elle modifié le Grand Canyon il y a 56 000 ans ?
miniature
🕒 Le lien surprenant entre repas tardifs, santé et prise de poids
miniature
💥 Cette collision de trous noirs est si massive qu'elle fait trembler nos lois de l'astrophysique
miniature
1
🩺 Cancer: des cellules "oubliées" passent à l'offensive
miniature
🔭 Quel est cet objet mystérieux, lié à Neptune dans une orbite jamais vue auparavant ?
miniature
🍄 Découverte surprenante: vivre 25 ans de plus grâce aux "champignons magiques" ?
miniature
🩺 L'âge des premières règles est un indicateur de la santé à venir
miniature
⚛️ Cette découverte pourrait expliquer pourquoi notre Univers existe
miniature
🌋 Découverte majeure sous Yellowstone grâce à l'IA
miniature
1
🏹 Violence préhistorique: découverte d'un surprenant homicide raté
miniature
🌌 Des scientifiques découvrent dans l'Univers un gigantesque filament de matière "manquante"
miniature
🐱 Ce chat a aidé à découvrir un virus inconnu... deux fois !
miniature
🪐 Cette planète provoque la fureur de son étoile
miniature
👂 Et si nous pouvions entendre une caresse ?
miniature
👑 Cette découverte archéologique révèle les prémices des pharaons
miniature
🦈 Le requin bleu peut changer de couleur, comme un caméléon
miniature
🌞 La NASA dévoile les images les plus proches jamais prises du soleil
miniature
⏳ Il est maintenant possible de mesurer le vieillissement avec précision
miniature
🚀 1 pétabit/seconde: ce nouveau record permet de télécharger tout le catalogue de Netflix en 1 seconde
miniature
🩺 Donald Trump et insuffisance veineuse chronique: une maladie aux complications graves
miniature
🌍 Les barrages construits par l'Homme ont déplacé les pôles de la Terre
miniature
🍖 Les Néandertaliens avaient leurs propres recettes de cuisine, qui veut goûter ?
miniature
🔭 À l'observatoire Rubin, le grand film de l'Univers démarre
miniature
🧬 Réparer l'ADN cassé et sauver nos cellules
miniature
🪨 Découverte d'un important gisement de "kryptonite" en Europe, au potentiel énergétique hors norme
miniature
🕰️ La Terre possède sa propre horloge géologique
miniature
☄️ Les scientifiques ne comprennent pas la trajectoire des fragments de l'astéroïde Dimorphos
miniature
🦖 Les protéines survivent bien plus longtemps que l'ADN, et pourraient réécrire l'histoire
miniature
📢 Pourquoi certains sons nous réveillent, et d'autres non ?
miniature
🌋 Des BLOBS se déplacent sous nos pieds: des structures à l'origine d'éruptions cataclysmiques
miniature
🌀 Une centaine de galaxies invisibles autour de la Voie lactée ?
miniature
🐛 Ces chenilles "plastivores" transforment le plastique en graisse corporelle
miniature
⛈️ La météo sur Titan vue par James Webb et Keck
miniature
💀 Cette pieuvre tue avec un venin 1200 fois plus toxique que le cyanure, et il n'y a pas d'antidote
miniature
👀 Une "Bête" géante observée en train de danser au-dessus du Soleil
miniature
⏳ Des séismes lents filmés pour la première fois en temps réel. De quoi s'agit-il ?
miniature
✨ Découverte "d'étoiles ratées" de l'extrême: que nous apprennent-elles ?
miniature
🎨 Pourquoi les hommes sont-ils beaucoup plus souvent daltoniens que les femmes ?
Page générée en 0.194 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise