Restez toujours informé: suivez-nous sur Google Actualités (icone ☆)
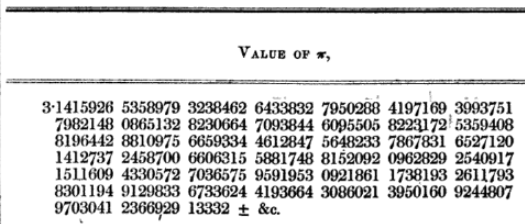
"Pi est un nombre irrationnel bien connu. Il apparaît très souvent dans des formules en mathématiques et en physique notamment, mais il est trop complexe pour le cerveau humain ‒ son expansion décimale s'allonge jusqu'à l'infini: 3,141592... On veut donc avoir une bonne approximation de Pi par une fraction simple", affirme Dimitrios Koukoulopoulos, professeur au Département de mathématiques et de statistique de l'Université de Montréal.
La conjecture de Duffin-Schaeffer, qui a été exposée en 1941, restait à être prouvée. C'est finalement l'exploit qu'a réussi Dimitrios Koukoulopoulos avec son collègue James Maynard, de l'Université d'Oxford, dans une collaboration qui a commencé au Mathematical Sciences Research Institute à Berkeley à l'hiver 2017 et qui s'est terminée à Oxford ce printemps.
"La conjecture de Duffin-Schaeffer est un problème central dans le domaine et nous avions envie de tenter notre chance parce que nous pensions avoir les outils nécessaires pour l'aborder", observe Dimitrios Koukoulopoulos.
Les deux complices sont des théoriciens des nombres, mais ils ne sont pas des experts de l'approximation de nombres irrationnels par des fractions. "Cela dit, je crois que c'était finalement un atout, puisque nous avons ainsi étudié le problème d'un nouveau point de vue", fait remarquer le professeur. Qu'est-ce que la conjecture de Duffin-Schaeffer ?
La conjecture de Duffin-Schaeffer porte sur les restrictions qu'on applique aux fractions, par exemple si l'on élimine le dénominateur 7 ou encore tous les nombres qui se terminent par 7. Si l'on n'utilise que les fractions restantes comme approximations, à quoi peut-on s'attendre comme qualité, soit la distance avec le nombre approximé, et comme complexité, qui correspond à la taille du dénominateur ?
"La conjecture de Duffin-Schaeffer dit que, lorsque les restrictions imposées sont assez faibles, on peut approximer presque tous les nombres, mais s'il y a trop de restrictions, on ne peut en approximer presque aucun, explique le professeur. Il n'y a pas d'entredeux."
Changer de perspective

Dimitrios Koukoulopoulos et James Maynard
"Le graphe aide à visualiser les relations entre les différents dénominateurs: on relie deux dénominateurs par une ligne lorsqu'ils partagent un grand facteur", mentionne Dimitris Koukoulopoulos.
Prenons les dénominateurs 10 et 15. Ils ont un grand facteur commun: le nombre 5. Cela crée beaucoup d'approximations doubles, soit des nombres qui peuvent être approximés avec des fractions à la fois sur 10 et sur 15, comme 3/10 et 4/15, qui sont très près. Dans le graphe, les dénominateurs 10 et 15 seront reliés par une ligne. Par contre, 7, qui n'a pas de facteur commun, ne sera relié ni à l'un ni à l'autre.
Lorsqu'il y a trop de connexions dans le graphe, cela signifie que le dénominateur a trop de facteurs communs et qu'il rendra l'approximation de plusieurs nombres difficile. Pourquoi ? Parce qu'on se retrouvera alors avec un petit bassin de nombres approximés par trop de fractions, tandis que la plupart des nombres n'auront aucune approximation. Donc, au final, il y aura trop de restrictions pour réaliser l'approximation de la majorité des nombres.
L'utilisation des méthodes de la théorie des graphes était complètement nouvelle dans le traitement de la conjecture de Duffin-Schaeffer. Elle a d'ailleurs certainement suscité bien des froncements de sourcils.
"Il y a toujours des doutes dans la communauté lorsque quelqu'un dit avoir résolu un vieux problème et c'est la bonne attitude à avoir, affirme M. Koukoulopoulos. Il faut bien examiner la démonstration."
Les répercussions de la démonstration
Cette avancée est encore en attente de publication ‒ elle en est à l'étape de la revue par les pairs ‒, mais elle a été annoncée en grande pompe au cours d'une conférence cet été en Italie. Puis, la nouvelle a été diffusée largement dans les médias européens et américains.
Une telle attention médiatique est rare dans la discipline, mais le passionné de mathématiques depuis la tendre enfance ne laisse pas le succès lui monter à la tête. Il réfléchit d'ailleurs déjà à d'autres problèmes qui pourraient être résolus grâce à la méthode élaborée avec James Maynard.
"Je veux prendre encore quelque temps pour penser aux répercussions de nos idées, indique-t-il avec un grand sourire qui dit tout. Pour le moment, notre méthode est assez flexible pour qu'on pense l'appliquer à d'autres problèmes."
Dimitrios Koukoulopoulos travaille notamment à comprendre les opérations de multiplication.
"Il y a des problèmes variés avec la multiplication, par exemple avec les nombres premiers, précise-t-il. C'est central dans la théorie des nombres. On veut comprendre comment ils sont répartis entre les nombres entiers, s'ils ont un motif d'apparence, etc."
Ces questions sont d'ailleurs liées à la conjecture de Duffin-Schaeffer parce qu'elles touchent toujours à la structure multiplicative des dénominateurs.
Celui qui dit parler peu de ses recherches avec ses proches, puisque "le langage mathématique est souvent peu accessible", se réjouit de l'intérêt suscité par cette découverte. Il ne ménage pas ses efforts d'ailleurs pour vulgariser le mieux possible ses travaux afin de réussir un rapprochement entre les mathématiques et les gens.
"Heureusement, j'ai eu de la chance avec ce travail parce que pratiquement tout le monde connaît le nombre Pi, alors ça pique la curiosité et ça facilite le rapprochement."