Approximation - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Une approximation est une représentation grossière c'est-à-dire manquant de précision et d'exactitude, de quelque chose, mais encore assez significative pour être utile. Bien qu'une approximation soit le plus souvent effectuée sur les nombres, elle est également fréquemment appliquée à des objets tels que des fonctions mathématiques, des formes géométriques, et des lois physiques.
Des approximations peuvent être employées lorsqu'un manque d'information nous empêche d'utiliser des représentations exactes. Par exemple, nous devons déterminer la vitesse moyenne d'un véhicule et nous ne connaissons pas sa vitesse instantanée mais seulement sa vitesse au départ et à l'arrivée. Par ailleurs, même lorsque la représentation exacte est connue, il peut être préférable d'employer une approximation qui simplifie l'analyse sans une trop grande perte d'exactitude.
Par exemple, les physiciens rapprochent souvent la forme de la Terre à celle d'une sphère, même si des représentations plus précises sont possibles. En effet, de nombreux phénomènes physiques, comme par exemple la pesanteur, sont plus faciles à étudier en considérant une sphère plutôt que des formes moins régulières.
Le type d'approximation utilisé dépend de l'information disponible, du degré d'exactitude exigé, de la sensibilité du problème à ses données, et du gain de temps et d'effort qui peut être réalisé par une approximation.
En science
La méthode scientifique est appliquée avec une constante interaction entre les lois scientifiques (théorie) et les mesures empiriques, qui sont constamment comparées les unes aux autres.
L'approximation se rapporte également à l'utilisation d'un processus plus simple. Ce modèle est employé pour faciliter des prévisions. En philosophie des sciences, il est souvent admis que les mesures empiriques ne sont rien de plus que des approximations; et elles ne représentent pas parfaitement les grandeurs mesurées. En histoire des sciences, il apparaît que les lois scientifiques généralement considérées comme vraies à une période de l'histoire deviennent plus tard de simples approximations d'un certain système de lois plus profondes.
À chaque fois qu'un nouveau système de lois est proposé, il est exigé que dans des situations limites dans lesquelles les anciennes lois étaient expérimentées, les nouvelles lois restent presque identiques aux anciennes, aux incertitudes près des mesures plus anciennes. C'est ce qui s'appelle le principe de correspondance.
En mathématiques
En mathématiques, le terme « approximation » peut renvoyer à :
- L'approximation de nombres : Les approximations numériques résultent parfois de l'emploi d'un nombre plus restreint de chiffres significatifs dans la représentation décimale d'un nombre. L'approximation diophantienne traite de l'approximation des nombres réels par les nombres rationnels. Le symbole
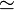
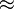
- L'approximation de fonctions : La théorie de l'approximation est une branche des mathématiques, représentant une partie importante de l'analyse fonctionnelle. Les équivalents traitent de l'approximation d'une fonction quand un paramètre tend vers une valeur donnée.
- L'approximation d'intégrales : Il existe également des méthodes numériques pour l'approximation des intégrales.
- L'approximation de solutions d'équations : De nombreuses méthodes existent pour approcher numériquement la solution d'une équation. Citons entre autres la méthode de Newton qui utilise les dérivées successives pour approcher les solutions d'une fonction. Pour les équations aux dérivées partielles, des solutions approchées peuvent être trouvées grâce à la méthode des éléments finis, ainsi que de nombreuses autres méthodes d'analyse numérique.

















































