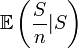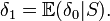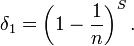Statistique - Définition et Explications

Introduction

Une statistique est, au premier abord, un nombre calculé à propos d'un échantillon. D'une façon générale, c'est le résultat de l'application d'une méthode statistique à un ensemble de données. Dans le calcul de la moyenne arithmétique (La moyenne arithmétique d'une série statistique est la moyenne ordinaire, c'est-à-dire le rapport de la somme d’une distribution d’un caractère...), par exemple, l'algorithme consiste à calculer la somme de toutes les valeurs des données et à diviser par le nombre (La notion de nombre en linguistique est traitée à l’article « Nombre grammatical ».) de données. La moyenne (La moyenne est une mesure statistique caractérisant les éléments d'un ensemble de quantités : elle exprime la grandeur qu'auraient chacun des membres de l'ensemble s'ils...) est ainsi une statistique (La statistique est à la fois une science formelle, une méthode et une technique. Elle comprend la collecte, l'analyse, l'interprétation de données ainsi que la présentation de ces ressources afin de les...). Pour être complet dans la description de l'utilisation d'une statistique (Une statistique est, au premier abord, un nombre calculé à propos d'un échantillon. D'une façon générale, c'est le résultat de...), il faut décrire à la fois la procédure et l'ensemble (En théorie des ensembles, un ensemble désigne intuitivement une collection d’objets (les éléments de l'ensemble),...) de données.

De façon formelle bien que cela soit rarement utilisé une statistique est une variable aléatoire (Une variable aléatoire est une fonction définie sur l'ensemble des résultats possibles d'une expérience aléatoire, telle qu'il soit possible de déterminer la probabilité pour qu'elle prenne une valeur donnée ou qu'elle prenne une...) d'un type particulier. C'est en effet une fonction d'un vecteur (En mathématiques, un vecteur est un élément d'un espace vectoriel, ce qui permet d'effectuer des opérations d'addition et de multiplication par un scalaire. Un n-uplet...) composée de plusieurs observations (L’observation est l’action de suivi attentif des phénomènes, sans volonté de les modifier, à l’aide de moyens d’enquête et d’étude...) d'une loi. Cela permet entre autres d'étendre aux statistiques un certain nombre de résultats sur les variables aléatoires entre autres le caractère indépendant de deux statistiques ou calculer des densités de statistiques.

Parmi les statistiques un certain nombre ont des propriétés particulières qui servent (Servent est la contraction du mot serveur et client.) entre autres en Inférence statistique (L'inférence statistique consiste à induire les caractéristiques inconnues d'une population à partir d'un échantillon issu de cette population. Les caractéristiques de l'échantillon, une...) pour l'estimation statistique. Les estimateurs servent, comme leur nom l'indique, à estimer des paramètres statistiques. L'optimisation de ces estimateurs peut également faire intervenir des statistiques auxiliaires vérifiant certaines propriétés et qui permettent de faire converger plus vite ces estimateurs.

Estimateurs

En statistique inférentielle (L'inférence statistique consiste à induire les caractéristiques inconnues d'une population à partir d'un échantillon issu de cette population. Les...), un estimateur est une valeur calculée sur un échantillon (De manière générale, un échantillon est une petite quantité d'une matière, d'information, ou d'une solution. Le mot est utilisé dans...) et que l'on espère être une bonne évaluation de la valeur que l'on aurait calculée sur la population totale. On cherche à ce qu'un estimateur soit sans biais, convergent ( en astronautique, convergent en mathématiques, suite convergente série convergente ), efficace et robuste.

Principales propriétés souhaitables

Si est un estimateur de θ on dit qu'il est:

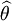
• Convergent si: tend en probabilité (La probabilité (du latin probabilitas) est une évaluation du caractère probable d'un évènement. En mathématiques, l'étude des...) vers θ quand le nombre d'observations augmente. Plus le nombre d'observations est grand et plus l'on se rapproche de la vraie valeur. Cette propriété d'un estimateur est essentielle si l'on veut pouvoir estimer avec grande précision le paramètre (Un paramètre est au sens large un élément d'information à prendre en compte pour prendre une décision ou pour effectuer un calcul.) θ. En effet, si c'est le cas, pour augmenter la précision de l'estimateur, il suffira d'effectuer plus de mesures.
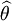
• Sans biais si: On peut voir un estimateur sans biais comme un estimateur pour lequel on ne fait pas d'erreur systématique (En sciences de la vie et en histoire naturelle, la systématique est la science qui a pour objet de dénombrer et de classer les taxons dans un certain ordre,...) pour une taille d'échantillon donnée (Dans les technologies de l'information (TI), une donnée est une description élémentaire, souvent codée, d'une chose, d'une transaction d'affaire, d'un événement, etc.). À contrario pour un estimateur qui aurait un biais il pourrait par exemple exister des valeurs du paramètre θ pour lesquelles on sur estimerait ou sous estimerait de façon systématique la grandeur que l'on cherche à évaluer. C'est pour qu'il soit sans biais que l'on estime d'ordinaire la variance ( En statistique et en probabilité, variance En thermodynamique, variance ) quand on a n observations par et non par σ² par exemple.

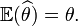
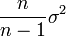
Ces deux propriétés sont essentielles et en règle générale on considère que tout (Le tout compris comme ensemble de ce qui existe est souvent interprété comme le monde ou l'univers.) estimateur devrait au moins vérifier ces deux propriétés pour qu'on puisse le considérer comme suffisamment précis. On peut de plus vouloir qu'un estimateur soit efficace (c'est-à-dire que l'estimation qu'il fournit varie le moins possible autour (Autour est le nom que la nomenclature aviaire en langue française (mise à jour) donne à 31 espèces d'oiseaux qui, soit appartiennent au genre Accipiter, soit constituent les 5 genres...) de la valeur à estimer) ou robuste (c'est-à-dire qu'il soit peu sensible aux variations d'une mesure sur les n). Ces deux propriétés sont détaillées plus bas dans les sections Optimisation d'estimateur et Robustesse.

Optimisation d'estimateurs

L'optimisation d'estimateurs peut se faire grâce à l'usage (L’usage est l'action de se servir de quelque chose.) de statistiques exhaustives. Une méthode possible pour trouver de "bons" estimateurs est de prendre un premier estimateur sans biais de la valeur à estimer sans trop chercher à l'optimiser. Ensuite on optimise cet estimateur en se servant de statistiques exhaustives.

Cette méthode repose principalement sur deux théorèmes : le théorème (Un théorème est une proposition qui peut être mathématiquement démontrée, c'est-à-dire une assertion qui peut être établie comme vraie au travers d'un raisonnement logique construit à partir d'axiomes. Un...) de Rao-Blackwell qui fournit un deuxième estimateur de meilleur qualité appelé estimateur augmenté et le théorème de Lehman-Scheffer qui donne des conditions suffisantes pour que cet estimateur soit optimal.

Estimateurs augmentés et Théorème de Rao-Blackwell

Si δ est un estimateur sans biais et S une statistique exhaustive alors l'estimateur augmenté a une variance plus faible que l'espérance de départ et est également sans biais. L'estimateur augmenté est donc toujours plus précis que l'estimateur initial si on l'augmente d'une statistique exhaustive.

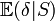
Dans le cas multiparamétrique où l'estimateur et le paramètre sont de dimension (Dans le sens commun, la notion de dimension renvoie à la taille ; les dimensions d'une pièce sont sa longueur, sa largeur et sa profondeur/son...) supérieure 1, on considère la matrice de variance-covariance. L'erreur quadratique du nouvel estimateur est toujours plus faible que celui de l'ancien estimateur et ce quelle que soit la norme (Une norme, du latin norma (« équerre, règle ») désigne un état habituellement répandu ou moyen considéré le plus...) utilisée. Même si les différentes composantes ne sont pas normées de la même façon l'estimateur augmenté est toujours préférable.

Exemple

On considère donc n variables aléatoires X_i distribués selon des lois de Poisson (Dans la classification classique, les poissons sont des animaux vertébrés aquatiques à branchies, pourvus de nageoires et dont le corps est le plus souvent...) de paramètre λ et l'on cherche à estimer e ^{− λ}. On peut montrer assez facilement en considérant le critère de factorisation que est une statistique exhaustive. Pour montrer l'intérêt de ce théorème, on prend un estimateur très grossier de e ^{− λ}: δ₀ = δ(X₁,0) qui vaut 1 si X₁ = 0 et 0 sinon. Cet estimateur ne prend en compte qu'une seule valeur de X alors qu'on en dispose de n et il ne donne pour résultat que 0 ou 1 alors que la valeur de e ^{− λ} appartient à l'intervalle ]0,1] et ne vaut sans doute pas 1. (si c'était le cas X_i vaudrait 0 de façon déterministe et on s'en serait aperçu en regardant les données). Pourtant malgré la grossièreté de cet estimateur, l'estimateur obtenu est très bon et on peut même montrer qu'il est optimal. L'estimateur augmenté vaut :

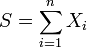
On peut montrer que:

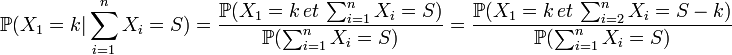
Et avec l'indépendance de X_i:

Si X_i suit une loi de poisson (En statistique, la loi de Poisson de paramètre λ, ou loi des événements rares, correspond au modèle suivant:) de paramètre λ alors la fonction génératrice (En mathématiques, la fonction génératrice de la suite (an) est la série formelle définie par) vaut . Avec les propriétés de la fonction génératrice on en déduit que la somme de n variables suivant des lois de poisson de paramètre λ est une loi de Poisson de paramètre nλ. On en déduit les probabilités et X₁ suis une loi binomiale (En mathématiques, une loi binomiale de paramètres n et p correspond au modèle suivant :) B(S, 1/n). La valeur en k=0 nous donne l'estimateur δ₁

 

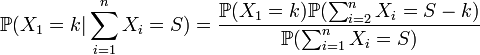
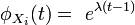
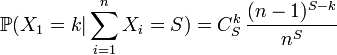
δ₁ est tout comme de δ₀ un estimateur de e ^{− λ} mais à l'avantage d'être beaucoup plus précis grâce à l'application du théorème de Rao–Blackwell. En fait, on montre avec Théorème de Lehman Scheffé qu'il est même optimal.

On remarquera entre autres que est un estimateur optimal de λ (cela se montre de la même manière) mais que l'estimateur pour e ^{− λ} est différent de . En fait, on peut même montrer que bien que soit un estimateur convergent de e ^{− λ} c'est un estimateur de relativement mauvaise qualité car il est biaisé et qu'en l'estimant de la sorte on fait une erreur systématique sur l'estimation. De façon générale, il peut être intéressant pour estimer f(λ) de construire un estimateur spécifique plutôt que de calculer la valeur prise par f par l'estimateur de λ.

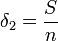
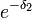
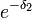
Statistique complète et Théorème de Lehman Scheffé

On dit qu'une statistique est complète (on dit parfois totale) si : implique f=0 presque partout.

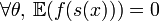
Le théorème de Lehman-Scheffé a une importance particulière en statistiques puisqu'il permet de trouver des estimateurs optimaux qui ne peuvent pas être améliorés en termes de précision car ils atteignent la borne FDCR. De tels estimateurs n'existent pas forcément mais si l'on dispose d'une statistique qui soit à la fois complète et totale et d'un estimateur δ qui soit sans biais alors l'estimateur augmenté est optimal et l'on ne peut pas trouver de meilleur estimateur.

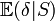
Exemple

Montrons par exemple que pour une loi exponentielle (La fonction exponentielle est l'une des applications les plus importantes en analyse, ou plus généralement en mathématiques et dans ses domaines d'applications. Il existe plusieurs définitions équivalentes : un morphisme continu de...) de paramètres λ la moyenne des observations est le meilleure estimateur possible pour λ. Si l'on a un vecteur des observations X de taille n avec les X_i de loi exponentielle (λ,σ) on commence par montrer que est une statistique exhaustive et complète.

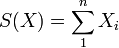
Pour montrer que cette statistique est exhaustive cela se fait relativement simplement grâce au théorème de factorisation. Pour montrer le fait que cette statistique est complète il faut utiliser l'injectivité de la transformée de Laplace.

Pour montrer que c'est bien une statistique complète il faut vérifier que:

implique bien que f=0 presque partout. Avec la définition (Une définition est un discours qui dit ce qu'est une chose ou ce que signifie un nom. D'où la division entre les définitions réelles et les définitions nominales.) d'une loi gamma s(x) suit une loi gamma de paramètre (n,λ) on a donc en remplaçant par la densité (La densité ou densité relative d'un corps est le rapport de sa masse volumique à la masse volumique d'un corps pris comme référence. Le corps de...) d'une loi gamma:

d'où: Par injectivité de la transformée de Laplace on en déduit donc que f(y)y^{n − 1} = 0 presque partout puis que f(y)=0 presque partout donc la statistique est bien complète.

 

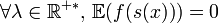
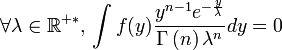
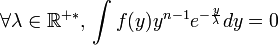
Une fois montré que la statistique S est à la fois complète et exhaustive l'estimateur de la moyenne étant égal à l'estimateur augmenté on en déduit immédiatement grâce au théorème de Lehman Scheffé que cet estimateur est optimal au sens (SENS (Strategies for Engineered Negligible Senescence) est un projet scientifique qui a pour but l'extension radicale de l'espérance de vie humaine. Par une évolution progressive allant du...) où il atteint la borne FDCR et que l'on ne peut en trouver de meilleur. L'estimateur de la moyenne est l'estimateur le plus précis que l'on puisse trouver pour le paramètre d'une loi exponentielle.