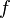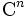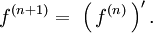Dérivation itérée - Définition

Soit une fonction de vers définie sur un intervalle de (non réduit à un point).

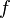
Dérivée première sur un intervalle

Lorsque la dérivée existe pour tout , on dit que est " dérivable sur  ".
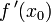
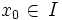
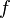
On définit dans ce cas la fonction .

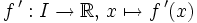
Cette fonction s'appelle la " fonction dérivée de sur  " ou " fonction dérivée première de sur  " et se note également .

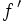
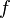
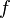
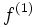
Dérivée seconde sur un intervalle

Lorsque est dérivable sur et que la fonction est elle-même dérivable sur , sa fonction dérivée sur , , s'appelle la fonction " dérivée seconde de sur  " et se note ou . On dit alors que est " dérivable deux fois sur  ".

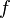
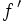
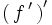
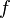
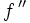
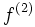
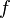
Dérivée n^e sur un intervalle

On définit par récurrence (sous réserve d'existence) les " dérivées successives de ƒ sur I " par l’égalité

La fonction ƒ⁽ⁿ⁾ (où n ≥ 1) est appelée fonction " dérivée n^e (ou d'ordre n) de ƒ sur I ".

Lorsqu'elle existe, on dit que ƒ est " dérivable n fois sur I ". Dans ce cas, toutes les dérivées successives de ƒ ayant un ordre strictement inférieur à n sont continues sur I, puisqu'elles y sont dérivables ; mais ƒ⁽ⁿ⁾ n'est pas nécessairement continue sur I : c'est ce qui motive la définition donnée infra des fonctions de classe Cⁿ.

Nota

On convient de définir la fonction dérivée d'ordre 0 de ƒ en posant ƒ⁽⁰⁾ = ƒ.

Classe Cⁿ

Soit n un entier naturel non nul. On dit que la fonction est de classe (ou n fois continûment dérivable) sur si elle est n fois dérivable sur et si la fonction est continue sur .

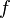
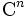
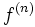
Conformément à la convention indiquée supra, la fonction est dite de classe sur si elle est continue sur .

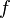
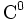
La fonction est dite de classe (ou indéfiniment dérivable) sur si pour tout , elle est dérivable n fois sur .
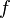
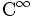
Cela revient à dire que pour tout , est de classe sur .