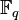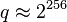Cryptographie sur les courbes elliptiques - Définition

En cryptographie, les courbes elliptiques, des objets mathématiques, peuvent être utilisées pour des opérations asymétriques comme des échanges de clés sur un canal non-sécurisé ou un chiffrement asymétrique, on parle alors de cryptographie sur les courbes elliptiques ou ECC (de l'acronyme anglais Elliptic curve cryptography). L'usage des courbes elliptiques en cryptographie a été suggéré, de manière indépendante, par Neal Koblitz et Victor Miller en 1985.

Les clés employées pour un chiffrement par courbe elliptique sont plus courtes qu'avec un système fondé sur le problème de la factorisation comme RSA. De plus l'ECC procure un niveau de sécurité équivalent ou supérieur aux autres méthodes. Un autre attrait de l'ECC est qu'un opérateur bilinéaire peut être défini entre les groupes. Cet opérateur se base sur le couplage de Weil ou le couplage de Tate. Les opérateurs bilinéaires se sont récemment vus appliqués de nombreuses façons en cryptographie, par exemple pour le chiffrement basé sur l'identité. Un point négatif est que les opérations de chiffrement et de déchiffrement peuvent avoir une plus grande complexité que pour d'autres méthodes.

La résistance d'un système fondé sur les courbes elliptiques repose sur le problème du logarithme discret dans le groupe correspondant à la courbe elliptique. Les développements théoriques sur les courbes étant relativement récents, la cryptographie sur courbe elliptique n'est pas très connue et souffre d'un grand nombre de brevets qui empêchent son développement.

Échange de clés

Alice et Bob se mettent d'accord (publiquement) sur une courbe elliptique , c'est-à-dire qu'ils choisissent une courbe elliptique . Ils se mettent aussi d'accord, publiquement, sur un point situé sur la courbe.

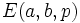
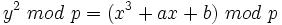
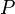
Secrètement, Alice choisit un entier , et Bob un entier . Alice envoie à Bob le point , et Bob envoie à Alice . Chacun de leur côté, ils sont capables de calculer qui est un point de la courbe, et constitue leur clef secrète commune.

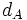
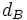
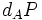
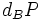
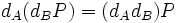
Si Eve a espionné leurs échanges, elle connaît . Pour pouvoir calculer , il faut pouvoir calculer connaissant et . C'est ce que l'on appelle résoudre le logarithme discret sur une courbe elliptique. Or, actuellement, si les nombres sont suffisamment grands, on ne connaît pas de méthode efficace pour résoudre ce problème en un temps raisonnable.

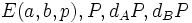
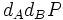
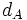
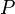
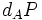
Implémentation

Paramètres du domaine

• Algorithme de Schoof

Longeur des clés

Pour une sécurité de 128 bits, on utilise une courbe sur le corps , où .