Bilinéaire - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Une application bilinéaire est un cas particulier d'application multilinéaire.
Définition
Soit E, F et G trois espaces vectoriels sur un corps

Soit
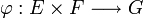

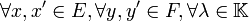
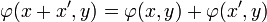
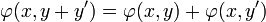
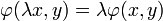
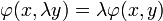
Si
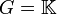
Exemple
Le produit scalaire est une forme bilinéaire, car il est distributif sur la somme vectorielle, et associatif avec la multiplication par un scalaire :
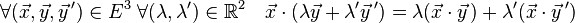
Espace euclidien • Espace hermitien • Forme bilinéaire • Forme quadratique • Forme sesquilinéaire • Orthogonalité • Base orthonormale • Projection orthogonale • Inégalité de Cauchy-Schwarz • Inégalité de Minkowski • Matrice positive • Matrice définie positive • Décomposition QR • Déterminant de Gram • Espace de Hilbert • Base de Hilbert • Théorème spectral • Théorème de Stampacchia • Théorème de Riesz • Théorème de Lax-Milgram • Théorème de représentation de Riesz


















































