La résolution des Sudoku, une affaire de couleurs...
Publié par Michel,
Source: Notices of the American Mathematical Society
Illustrations: Techno-science.net d'après Agnes M. Herzberg et M. Ram MurtyAutres langues:
Source: Notices of the American Mathematical Society
Illustrations: Techno-science.net d'après Agnes M. Herzberg et M. Ram MurtyAutres langues:
18
Restez toujours informé: suivez-nous sur Google Actualités (icone ☆)
Ces questions et d'autres sont explorées dans l'article Sudoku Squares and Chromatic Polynomials d'Agnes M. Herzberg et M. Ram Murty, paru dans l'édition de juin-juillet des Notes de l'AMS (American Mathematical Society) dans lequel les auteurs utilisent des outils mathématiques de la théorie des graphes pour analyser systématiquement des problèmes de Sudoku. Ils y démontrent également que l'analyse de ce type de problèmes conduit vers certains problèmes non résolus de cette théorie.
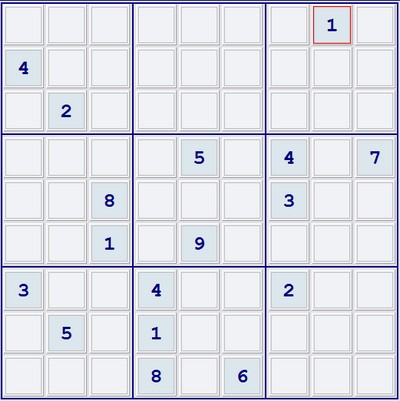
Un problème de Sudoku à solution unique, dont 17 chiffres sont donnés
Dans ce contexte, un "graphe" est un ensemble de noeuds reliés par des segments. On peut représenter les 81 cases d'un Sudoku comme les 81 noeuds d'un graphe, et l'on attribue à chacun des chiffres de un à neuf une couleur différente. Dans un graphe de Sudoku, deux noeuds sont reliés par un segment si les deux cases qu'ils représentent appartiennent à une même ligne, une même colonne, ou à un même bloc de 3 sur 3 cases. Puisque aucune ligne, aucune colonne, ni aucun bloc ne doit contenir plus d'une fois le même chiffre, le graphe ne possédera aucun noeud relié à un nœud de la même couleur. (Par exemple, en supposant que l'on représente le 1 avec la couleur rouge, deux noeuds rouges reliés par un segment signifieraient qu'une ligne, une colonne, ou un bloc posséderait deux 1, ce qui est interdit par la règle du Sudoku).
Dans le langage de la théorie des graphes, un graphique coloré sans connexion entre les noeuds de même couleur est appelé une "coloration propre". Ce que les amateurs de Sudoku tentent de réaliser chaque jour est d'étendre un graphe partiellement coloré à un graphe à coloration propre (le puzzle initial avec ses cases vides signifie que le graphe le représentant possède des nœuds qui demandent à être coloriés).
L'analogie entre les Sudoku et les graphes étant en place, Herzberg et Murty ont pu utiliser des outils de théorie des graphes pour démontrer des théorèmes sur ce type de problèmes. Par exemple, ils démontrent que le nombre de façons différentes d'étendre une coloration partielle est donné par un polynôme. Si la valeur de ce polynôme est zéro pour un Sudoku donné, alors le puzzle n'a aucune solution ; si la valeur est 1, le puzzle n'a qu'une solution ; et ainsi de suite. Ils démontrent également que, pour qu'un Sudoku quelconque puisse n'avoir qu'une solution unique, au moins 8 des 9 chiffres doivent apparaître dans le problème posé ; si seulement 7 chiffres apparaissent, alors le puzzle possède au moins deux solutions. Et ceci évoque une question mathématique non résolue: "il serait extrêmement intéressant de déterminer sous quelles conditions une coloration partielle peut être étendue à une coloration [propre] unique", écrivent les auteurs.
Certains Sudokus sont plus difficiles à résoudre que d'autres, les plus ardus ne contenant que très peu de chiffres au départ. La détermination de ce nombre minimum d'entrées nécessite de s'assurer qu'un problème n'a qu'une seule solution. Herzberg et Murty donnent un exemple d'un Sudoku avec 17 entrées qui ne possède qu'une solution (grille ci-dessus). Aussi le nombre minimum est au plus 17. Cependant cela pourrait être 16 ou plus petit encore, mais personne ne le sait. On pourrait penser par ailleurs qu'un problème avec de nombreux chiffres donnés au départ est susceptible de n'avoir qu'une seule solution, mais ce n'est pas forcément le cas. L'article donne l'exemple d'un puzzle à 29 chiffres donnés qui possède au final deux solutions différentes (grille ci-dessous).
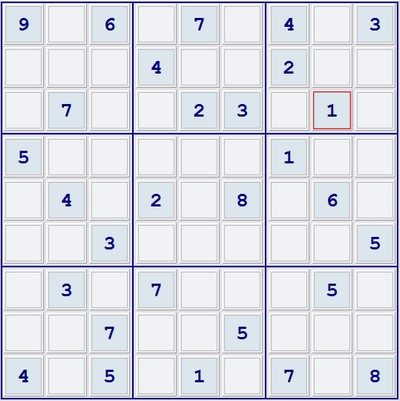
Un problème de Sudoku à deux solutions, dont 29 chiffres sont donnés
Et si vous vous demandez quand votre revue préférée manquera de problèmes de Sudoku, les auteurs affirment que le nombre de Sudoku distincts se situe quelque part autour de 5,5 milliards, ce qui devrait s'avérer suffisant pour occuper les afficianados pendant de nombreuses années encore.