Différente - Définition
La liste des auteurs de cet article est disponible ici.
En mathématiques, la différente est définie en théorie algébrique des nombres pour mesurer l'éventuel défaut de dualité d'une application définie à l'aide de la trace, dans l'anneau des entiers d'un corps de nombres algébriques
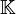
Si OK est l'anneau des entiers de
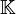
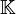
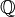
est une forme quadratique entière sur OK. Son discriminant comme forme quadratique n'est pas forcément +1 (en fait ceci arrive seulement pour le cas
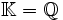
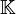
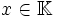
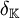
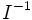
La norme de
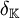

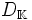
La différente peut aussi être définie pour une extension de corps de nombres L/K (la différente relative) et pour les corps locaux. Elle joue un rôle dans la dualité de Pontryagin pour les corps p-adiques.