Théorie des graphes - Définition
Le terme de graphe désigne en mathématiques une opération d'application. Il possède deux acceptions :
- le graphe d'une fonction (à distinguer de sa représentation graphique)
- un objet représentant une relation binaire, orientée ou non, entre des éléments d'un ensemble (dans le cas de relations entre plusieurs éléments, on parle d'hypergraphe).
La théorie des graphes concerne cette seconde acception.
Historiques
Jalons théoriques
Un des premiers résultats importants de la théorie des graphes est apparu dans les articles de Leonhard Euler avec le problème des sept ponts de Königsberg, publié en 1736. Il est aussi considéré comme un des premiers résultats topologiques en géométrie ; en effet, il ne dépend d'aucune mesure. Ces faits caractérisent la relation profonde qui existe entre la théorie des graphes et la topologie.
En 1835, Gustav Kirchhoff a publié ses lois des circuits pour calculer la tension et le courant dans un circuit électrique.
En 1852, Francis Guthrie a énoncé le problème des quatre couleurs étudiant la possibilité de colorier, en utilisant uniquement quatre couleurs, n'importe quelle carte géographique de telle façon que deux pays qui présentent une frontière commune soient de couleur distincte. Ce problème a été résolu par Kenneth Appel et Wolfgang Haken en 1976, soit un siècle après son énonciation ; il peut être considéré comme le point de naissance de la théorie des graphes. De nombreux termes et concepts théoriques fondamentaux de la théorie des graphes ont découlé des tentatives de résolution de ce problème.
Fondements contemporains
Plus récemment (années 1960), Claude Berge a posé les bases de la théorie moderne des graphes.
La première définition formelle d'un graphe n'est plus usitée à cause de sa lourdeur. À l'origine, Claude Berge définit un graphe par un ensemble de sommets, un ensemble d'arêtes et une fonction d'incidence qui associe deux sommets à chaque arête. Une arête est appelée une boucle si ses deux sommets sont identiques. Une arête est dite multiple s'il existe au moins une autre arête avec les mêmes sommets, sa multiplicité étant le nombre total d'arêtes ayant ces sommets.
Un graphe est dit simple s'il n'a ni boucle ni arête multiple. Le nombre maximum d'arêtes d'un graphe simple est donc 
, où n est le nombre de sommets.
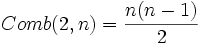
Présentation informelle
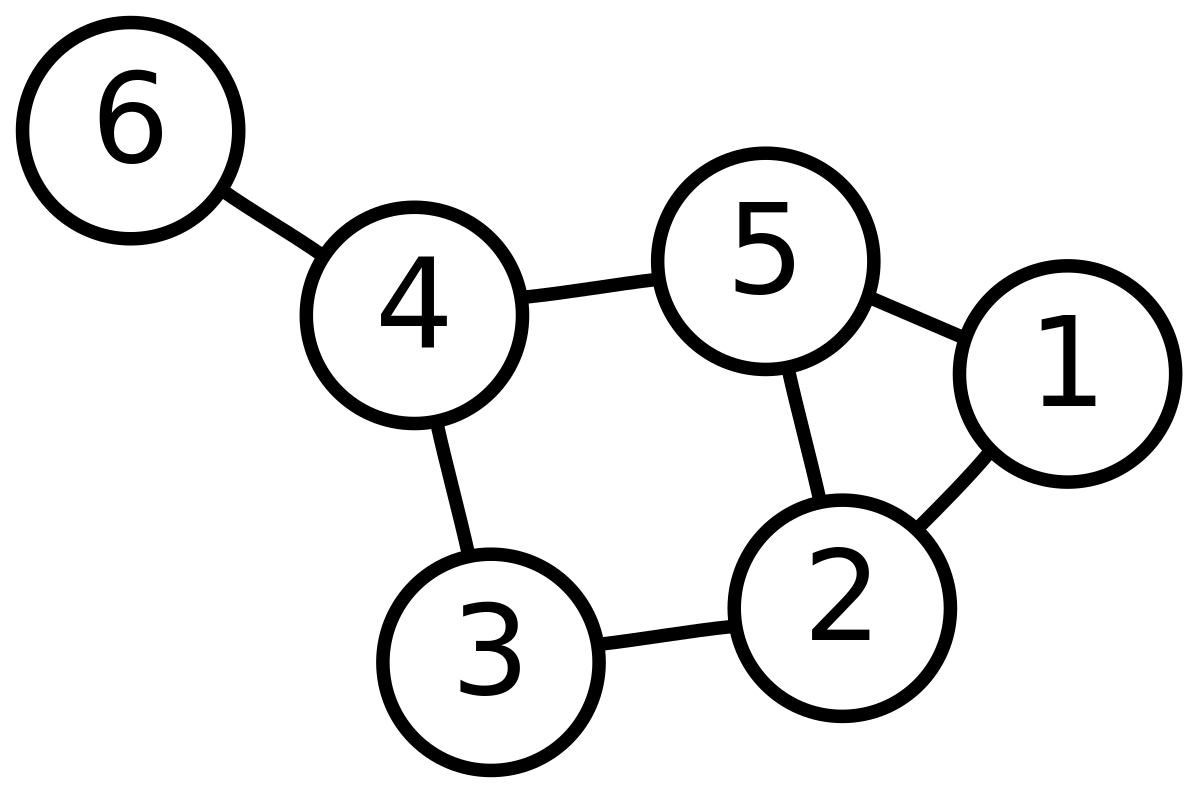
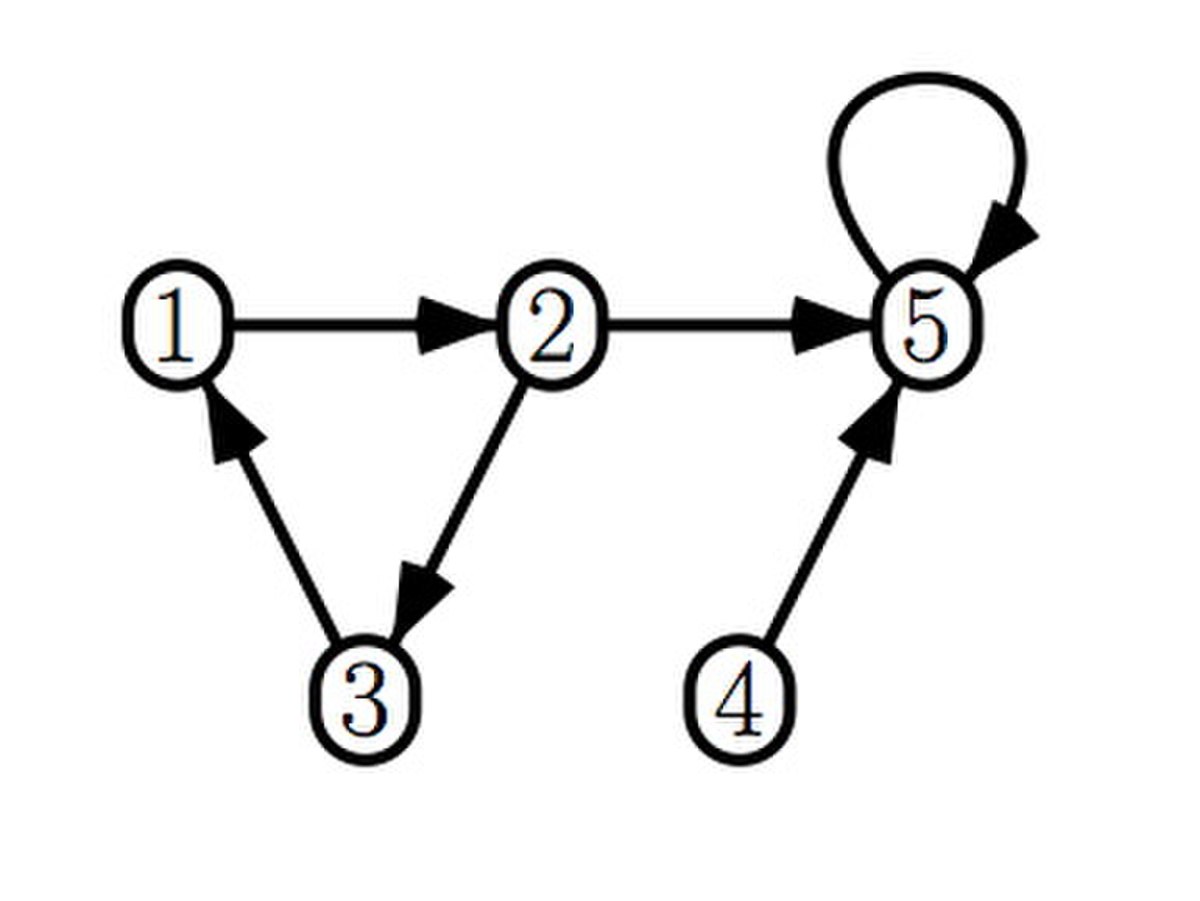
Un graphe possède des sommets et des arcs (ou arêtes). Un arc relie deux sommets entre eux : un sommet de départ et un sommet d'arrivée. Sur un dessin, on peut représenter les sommets par des points (ou des cercles) et les arcs par des flèches.
Les graphes peuvent servir à modéliser, entre autres :
- Un réseau routier à grande échelle : chaque ville est un sommet, chaque route entre deux villes est un arc (si elle ne passe pas par une autre ville), et même en général deux arcs : un dans chaque sens si la route n'est pas à sens unique.
- Un réseau routier à petite échelle : chaque intersection est un sommet, chaque tronçon de rue entre deux intersections est un arc.
- Un réseau de bus, un réseau ferré, ...
- Un réseau social.
- Le web : chaque page est un sommet, chaque lien hypertexte est un arc (de la page qui le contient vers la page pointée).
- Beaucoup de systèmes discrets : qui passent d'un état à un autre de façon discontinue au cours du temps, par des sauts. Voir automate fini et système de transition d'états.
- En mécanique du solide, le graphe des liaisons est un outil d'aide à la modélisation cinématique des mécanismes. Les propriétés du graphe ont parfois une signification (nb de cycle, classe etc.).
- En électronique, il peut servir à déterminer le nombre d'équations indépendantes (loi des mailles) disponibles.
Les graphes sont beaucoup utilisés en informatique.
Outre leur efficacité dans la modélisation programmatique de structure de données complexes, on les rencontre par exemple pour :
- les bases de données : un modèle relationnel de données est représentable par un graphe orienté regroupant des relations (sommets du graphe) et des dépendances (arcs du graphe). On parle notamment de graphe sémantique normalisé pour désigner un schéma de données relationnel résultant du processus de normalisation ;
- le Web sémantique : une ontologie se décrit comme un ensemble de concepts (sommets du graphe orienté) et de relations (arcs du graphe) ;
- le parallélisme : les techniques d'optimisation d'algorithme ou de détermination d'ordre d'exécution cohérente dans ce domaine prennent souvent en entrée des graphes de dépendance de flot d'instructions ou de données, où les sommets sont respectivement des instructions (de code à exécuter) et des données (initiales ou calculées) et les arcs des relations de dépendance temporelle (telle instruction doit s'exécuter après telle autre ; telle donnée doit être calculée avant telle autre).
Définitions élémentaires
Il existe différents types de graphes. La définition la plus générale est celle du graphe non orienté donnée ci-dessous :
- Un graphe non orienté G est un couple (S, A), où :
- S est un ensemble dont les éléments sont les sommets ;
- A est un ensemble de paires (non ordonnées) de sommets, appelées arêtes.
Une autre définition, celle du graphe orienté, est couramment utilisée :
- Un graphe orienté G est un couple (S, A), où :
- S est un ensemble dont les éléments sont les sommets ;
- A est un ensemble de couples (ordonnés) de sommets, appelés arcs.
Pour le graphe ci-dessus, on aurait 
et 
.
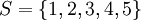
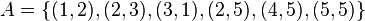
D'autres types de graphes existent. On cite notamment :
- Le multigraphe ou p-graphe : au plus p arcs (resp. arêtes) peuvent relier deux sommets. On peut le définir par une application de
dans 
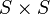
. - Le graphe valué : à tout arc (resp. arête) est associée une valeur (par exemple : un poids, un coût, une distance, ...). On parle de fonction de valuation définie de dans
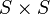
. - L' hypergraphe : un (hyper-)arc (resp. arête) peut relier plus de deux sommets entre eux. L'ensemble A des (hyper-)arcs (resp. arêtes) vérifie :
où Si désigne le produit cartésien de i occurrences de S.
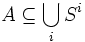
En informatique, de nombreuses implémentations de graphes existent. On peut par exemple numéroter les sommets, puis donner les arcs sous la forme d'une liste de couples. On peut aussi utiliser une matrice d'adjacence, plus rapide mais exigeant plus d'espace mémoire. Enfin, on peut associer à chaque sommet une liste d'adjacence, c'est-à-dire une liste contenant tous les sommets vers lesquels pointent les arêtes partant de ce sommet.
Exemples de représentation par des graphes
- Le graphe du web peut être modélisé par un graphe orienté dont les sommets sont des pages web et un arc représente un lien hypertextuel qui pointe d'une page vers une autre.
- Un réseau routier peut se représenter comme un graphe — non orienté, sauf si on tient compte d'éventuelles voies à sens unique — dont les sommets sont les villes et les arêtes les routes qui mènent directement d'une ville à une autre sans passer par une ville intermédiaire.
- Un réseau de neurones formels peut se représenter par un graphe orienté, valué — chaque arc porte une valeur — et dont chaque sommet est valué aussi de son seuil d'activation.
- Le réseau internet est un graphe dont les sommets sont les serveurs et les utilisateurs, et les arêtes les différentes interconnexions.
|
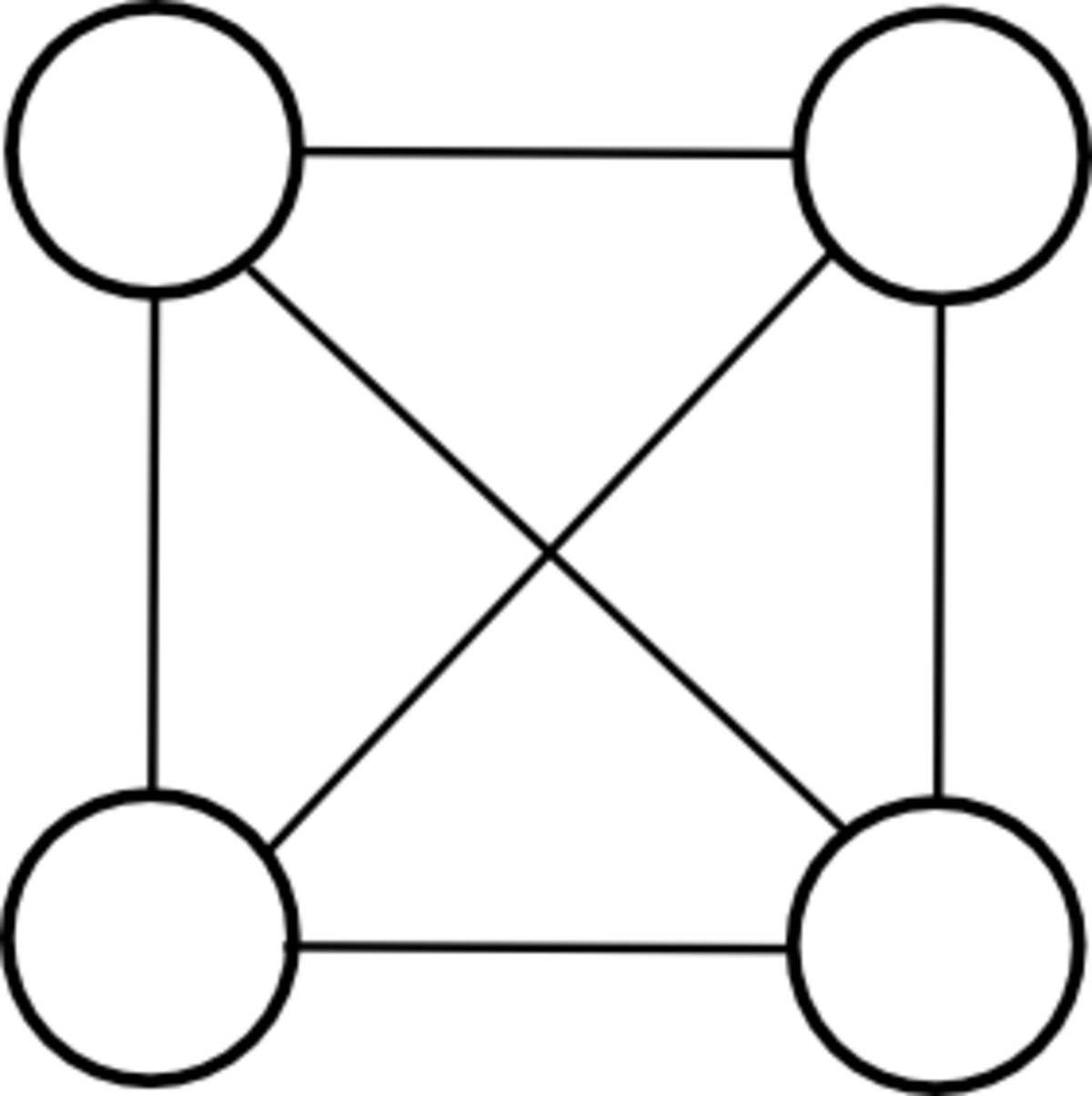
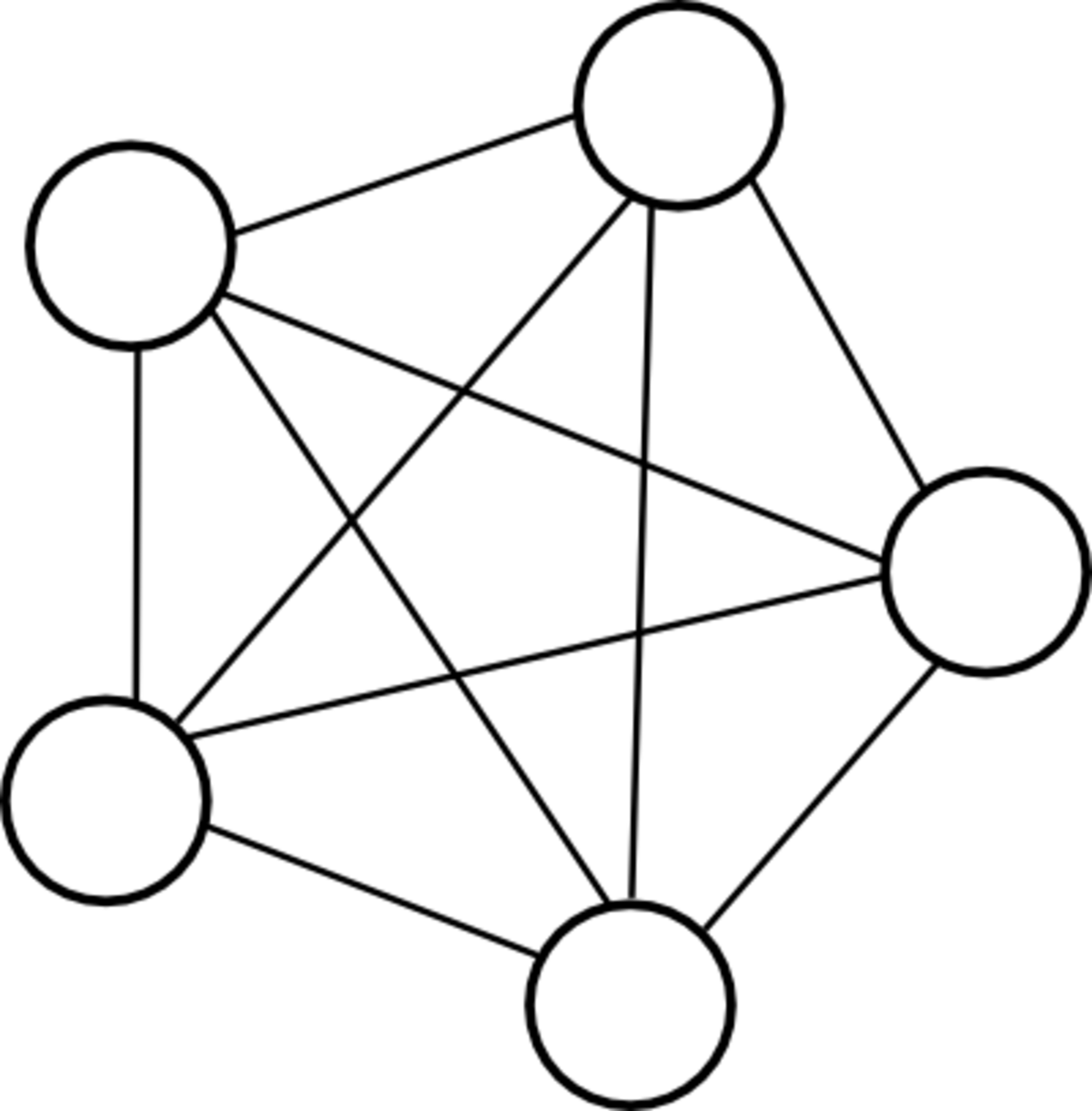
Graphes complets à 1, 2, 3, 4 et 5 sommets.
|
 |
 |
 |
 |
 |
Champ d'utilisation
La théorie des graphes étudie les propriétés de ces objets. Parmi les problèmes classiques figurent :
- Le problème des sept ponts de Königsberg ou la recherche de cycles eulériens.
- La connexité : existe-t-il un chemin reliant deux sommets ?
- L'arbre couvrant de poids minimal.
- Le plus court (respectivement: le plus long) chemin entre deux sommets d'un graphe valué.
- La coloration de graphe avec un nombre fixé de couleurs.
- Les sous-graphes denses maximaux (parfois appelés cliques).
- Les problèmes de flots maximaux ou minimaux.
- L'allocation de ressources.
- Le problème du voyageur de commerce (terme anglais : TSP — travelling salesman problem).
- Le problème du postier chinois.
- La décomposition d'un graphe en niveaux.
- La gestion de projet avec le réseau PERT.
- Les graphes hamiltoniens et hypo-hamiltoniens.
Cette théorie est fortement liée à l'algorithmique et à la complexité.
Quelques problèmes algorithmiques importants de la théorie des graphes
- Coloration (des sommets)
- Donnée : un graphe G = (S,A) non orienté et un entier positif k;
- Question : existe-t-il une fonction de S dans
telle que si deux sommets a et b de G sont adjacents alors 
?
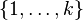
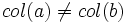
- Isomorphisme de graphes
- Donnée : deux graphes G = (S,A) et G' = (S',A')
- Question : Les graphes G et G' sont-ils identiques à un renommage de leurs sommets près? Ou plus formellement, existe-t-il une fonction bijective
telle que 
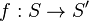
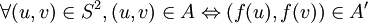
La complexité théorique de ce problème n'est, à ce jour, pas complètement établie. Il n'a jamais été montré que le problème appartenait à la classe des problèmes NP-complets mais aucun algorithme de résolution de complexité polynomiale n'a été trouvé. En pratique, ce problème est généralement simple. L'algorithme Nauty, basé sur la théorie des groupes, résout très efficacement ce problème. Il existe des algorithmes polynomiaux pour certains graphes particuliers (graphes à connexité bornée, arbres, graphes planaires...).
- Isomorphisme de sous-graphe partiel
- Donnée : deux graphes G = (S,A) et G' = (S',A') tels que
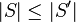
- Question : Le graphe G est-il "inclus" dans le graphe G' à un renommage de ses sommets près? Ou, plus formellement, existe-t'il une fonction injective telle que
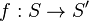
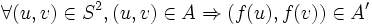
Ce problème est NP-complet dans le cas général. Il existe des algorithmes polynomiaux pour certains graphes particuliers, comme les arbres.
- Isomorphisme de sous-graphe non partiel
- Donnée : deux graphes G = (S,A) et G' = (S',A') tels que
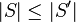
- Question : Le graphe G est-il "identique" à un sous-graphe du graphe G' à un renommage de ses sommets près? Ou plus formellement, existe-t'il une fonction injective telle que . Ce problème est un cas particulier de l'isomorphisme de sous-graphe (partiel) où la contrainte suivante est ajoutée : un couple de sommets du graphe G ne formant pas un arc ne peut être mis en correspondance par la fonction f qu'avec un couple de sommets du graphe G ne formant pas un arc également.
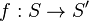
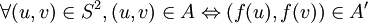
Ce problème est NP-complet dans le cas général. Il existe des algorithmes polynomiaux pour certains graphes particuliers, comme les arbres.
- Plus grand sous-graphe commun à deux graphes
- Donnée : deux graphes G = (S,A) et G' = (S',A')
- Question : Trouver la taille (généralement en terme de nombre de sommets) du plus grand graphe G'' tel que G'' soit un sous-graphe de G = (S,A) et de G' = (S',A').
Ce problème est NP-difficile.
Critiques
Alain Connes considère que les connaissances sur la théorie des graphes ne forment une théorie mais "un savoir, une série de faits"[1].