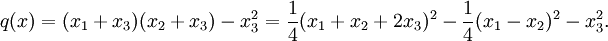Dimanche 12 Octobre 2025
Rechercher 🔍

Réduction de Gauss - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
- Introduction - Enoncé - Applications - Exemples

Exemples

  • Soit q\, une forme quadratique sur l'espace vectoriel \R^3 définie par

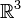
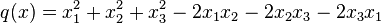
q(x)=x_1^2+x_2^2+x_3^2-2x_1x_2-2x_2x_3-2x_3x_1\,

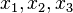
(On a désigné par x_1,x_2,x_3\, un élément x\, de \R^3 )


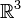
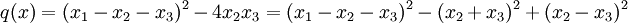
Alors \quad q(x)=(x_1-x_2-x_3)^2-4x_2x_3=(x_1-x_2-x_3)^2-(x_2+x_3)^2+(x_2-x_3)^2 .

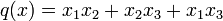
  • Autre exemple : q(x)=x_1x_2+x_2x_3+x_1x_3\,

On a alors q(x)=(x_1+x_3)(x_2+x_3)-x_3^2= \frac{1}{4}(x_1+x_2+2x_3)^2-\frac{1}{4}(x_1-x_2)^2-x_3^2.

Applications
- Introduction - Enoncé - Applications - Exemples
miniature
🦴 La pollution plastique pénètre jusque dans nos os
miniature
🔭 Cet algorithme rend les télescopes terrestres au niveau des télescopes spatiaux
miniature
🐧 Le mystère du manchot géant qui peuplait la Nouvelle-Zélande il y a 3 millions d'années
miniature
⏳ Pourquoi les femmes vivent plus longtemps que les hommes ?
miniature
🌩️ Découvrez le bulletin météo d'une étoile ratée
miniature
❄️ Peut-on prévoir un hiver rude grâce à l'automne ?
miniature
📡 Découverte dans l'espace d'un étrange et puissant double cercle radio
miniature
🍽️ Comment la faim modifie nos comportements: une plongée dans le cerveau
miniature
🌀 Une technique d'analyse innovante pour cartographier la matière noire dans l'histoire de l'Univers
miniature
🐊 Un ancien mini-crocodile découvert aux Etats-Unis
miniature
🔭 Vénus pourrait nous bombarder à distance: une menace invisible pour la Terre
miniature
🥱 Pourquoi bâille-t-on, et est-ce vraiment contagieux ?
miniature
🌲 De l'or pousse littéralement sur ces arbres
miniature
🧠 La carte cérébrale complète de nos prises de décision
miniature
🚀 L'hélium-3 lunaire: la nouvelle ruée vers l'or spatial
miniature
🐝 Des guêpes dans les figues ? Ce que dit la science...
miniature
🪐 Cette planète errante dévore 6 milliards de tonnes de matière par seconde !
miniature
🍄 Pourquoi voit-on des champignons partout en automne ?
miniature
🌋 Le mystère des couronnes de Vénus enfin percé ?
miniature
💤 À quoi servent les rêves ? Ce que fait votre cerveau pendant la nuit
miniature
🪙 Or et bijoux: un trésor de 1400 ans découvert près du lac de Tibériade
miniature
🩻 Une nouvelle technique d'imagerie médicale pour voir au cœur du vivant
miniature
☄️ Les missions spatiales détournées pour traquer l'objet venu d'ailleurs 3I/ATLAS
miniature
⌛ Le temps profond de la Terre serait... fractal
miniature
1
🧬 Transformer des cellules de peau en ovules: espoir pour les couples infertiles ou homosexuels
miniature
🦎 Découverte d'un reptile hybride lézard-serpent en Écosse !
miniature
🔭 Cette galaxie hybride chamboule toutes les classifications astronomiques
miniature
🍃 Pourquoi l'automne est-il plus venteux que l'été ?
miniature
🔬 Une vie extraterrestre dans Encelade ? Une découverte intrigante dans les archives de Cassini...
miniature
🌍 Accélération des bouleversements en Antarctique: une convergence de signaux alarmants
miniature
🌗 C'est prouvé: la face cachée de la Lune n'a rien à voir avec la face visible
miniature
🌍 Qui a vraiment découvert l'Amérique ?
miniature
🦝 Un animal encore jamais vu découvert dans les Andes péruviennes
miniature
🤢 Pourquoi les médicaments ont-ils si mauvais goût ?
miniature
🔭 Le mystérieux halo invisible de la Terre enfin révélé par un observatoire spatial
miniature
🌳 Les arbres d'Amazonie grossissent à vue d'œil à cause du CO2
miniature
🔭 James Webb capture le jet jumeau du trou noir de la galaxie M87
miniature
💎 Découverte de deux diamants "impossibles"
miniature
💑 Pourquoi les couples partagent souvent les mêmes troubles mentaux ?
miniature
☄️ Un inattendu astéroïde géocroiseur vient de frôler la Terre à 400 km
miniature
🦠 Détecter le cancer colorectal avec une IA et nos propres bactéries
miniature
🌋 Pour la première fois, le cœur d'un volcan actif imagé en 3D
miniature
🧠 Pourquoi notre cerveau adore les théories du complot ?
miniature
👜 Découverte exceptionnelle: la boîte à outils d'un chasseur préhistorique vieille de 30 000 ans
miniature
🧂 Une alimentation riche en sel provoquerait une inflammation du cerveau
miniature
🟠 Des structures anciennes de tailles kilométriques découvertes dans les profondeurs de Mars
miniature
🕷 Ce robot-araignée explore les intestins avec une agilité sans pareille
miniature
⚛️ Quantique: pour la première fois, des physiciens contournent le principe d'incertitude de Heisenberg
miniature
🧬 Une architecte de l'ADN déchue au travers de l'évolution
miniature
1
🔭 Au centre de cette photographie, de la pure matière noire ?
Page générée en 0.125 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise