Synthèse miroir-dioptre-lentille - Définition
Cet article synthétise la formule mathématique utilisable en optique géométrique et généralisant les formules obtenues pour un miroir, un dioptre et une lentille.
La formule
- ƒo /xo + ƒi /xi = 1
est une forme de la relation de Descartes qui fonctionne pour les miroirs, dioptres et lentilles ; elle s'écrit
- xi = ƒi xo /(x - ƒo )
ou encore
- (xi - ƒi )(x0 - ƒo ) = ƒi ƒo
-
- Le grandissement
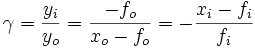
- Le grandissement
En fait, on peut appliquer la formule pour le dioptre dans tous les cas, en considérant
- n = -1 pour un miroir, ƒo = -ƒi /-1 ;
- n = 1 pour une lentille, ƒo = -ƒi /1 ;
C a pour coordonnées (ƒi + ƒo ,0).
Le grandissement γ vaut
- γ = yi /yo = -ƒo /(xo - ƒo ) = -(xi - ƒi )/ƒi
ceci permet de constater que le lieu de l'image yi est la droite d'équation
- y =(-yo /ƒi )·(xi - ƒi )
qui passe par le point (ƒi ,0) et de pente -yo /ƒi .

















































