Dioptre - Définition
En optique, un dioptre est une surface séparant deux milieux transparents d'indices de réfraction différents. Si la lumière se propage en ligne droite dans un milieu homogène et isotrope, elle est déviée lors du passage d'un dioptre : il y a réfraction.
De façon générale, il y a à la fois réfraction et réflexion : une partie de la lumière est réfléchie à la surface du dioptre et l'autre partie est réfractée lors de son passage dans l'autre milieu.
Le changement de direction au niveau du dioptre est décrit par les lois de Snell-Descartes qui fondent l'optique géométrique. Ces lois peuvent se représenter graphiquement en les appliquant à un rayon unique - dit incident - interceptant le dioptre en un point dit point d'incidence. Pour comprendre l'effet d'un dioptre sur la lumière, il faut considérer un nombre minimal de rayons de façon à représenter le faisceau de lumière.
Dioptre plan
Question de stigmatisme
Une des conséquences des lois de Snell-Descartes est que le dioptre plan est un système non-stigmatique. L'illustration ci-dessus montre que la lumière issue d'un point placé dans un aquarium, par exemple, donne des rayons réfractés dans l'air qui ont des directions sans point commun.
Pourtant, lorsqu'on regarde un poisson, on le voit bien ! C'est donc que l'œil du poisson, par exemple, constitue un objet lumineux qui forme une image sur la rétine de l'œil de l'observateur. Ceci n'est possible que parce que le faisceau de lumière est suffisamment étroit pour que la tache sur la rétine apparaisse comme un point. On est bien alors dans un cas de stigmatisme approché.
C'est ce phénomène qui permet d'expliquer l'expérience du " bâton brisé " que l'on montre en général pour illustrer la réfraction.
Réfraction limite et réflexion totale
On voit que si n1 > n2 (par exemple passage de l'eau vers l'air), alors pour des valeurs de sin(θ1) proches de 1, c'est-à-dire pour des incidences rasantes (rayon incident proche de la surface), on obtient par cette formule une valeur de sin(θ2) supérieure à 1 ! Ceci est évidemment impossible, cela correspond à des situations ou il n'y a pas de réfraction mais uniquement de la réflexion ; on parle de réflexion totale
L'angle limite de réfraction est donc tel que :
- sin(θlim) = n2/n1
Cette propriété est mise à profit dans certains systèmes réflecteurs (prisme à réflexion totale) et les fibres optiques.
Dioptre sphérique
Cas général
L'application des lois de Snell-Descartes permet également de traiter le cas des dioptres non plan. Il suffit de considérer localement la normale au dioptre point d'incidence de chaque rayon contribuant au faisceau.
De nouveau, par construction géométrique, on constate que le dioptre sphérique n'est pas stigmatique, sauf évidemment pour son centre, puisque chaque rayon arrivant perpendiculairement au dioptre n'est pas dévié. L'image du centre est alors le centre lui-même. (En fait, il est également stigmatique pour deux autres points particuliers de l'axe optique, appelés points de Weierstrass).
Dioptre sphérique dans les conditions de Gauss
Lorsqu'une faible partie du dioptre est utilisé ou, autre façon de dire, lorsque le rayon de courbure est très grand devant les dimensions liées à l'objet (taille, distance), on peut se placer dans les conditions dites de Gauss : on ne considère alors que les rayons qui passent près de l'axe et qui sont peu inclinés. La conséquence mathématique est la possibilité d'assimiler les sinus à la valeur des angles (en radian) et la conséquence physique est que l'on est alors dans les conditions d'un stigmatisme approché: dès lors, à un point objet, on peut associer un point image.
Ceci est particulièremet important pour la fabrication des lentilles (voir ci-après).
En particulier, on peut définir un foyer, image d'un objet à l'infini, c'est-à-dire autrement, point de convergence (ou de divergence) d'un faisceau incident parallèle à lui-même et parallèle à l'axe. Et plus généralement, on peut écrire une relation de conjugaison entre un point A de l'axe et son image A' donnée par le dioptre.
Les dioptres sphériques sont alors représentés de façon conventionnelle :
La relation de conjugaison ci-dessous permet de préciser les positions des foyers. Suivant la courbure (concave/convexe) et suivant le rapport des indices (n'> n ou n' < n) les foyers sont réels ou virtuels.
Pour un point A sur l'axe (orienté), le point image A' est tel que :
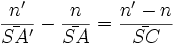
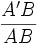
Applications
Les applications sont, de façon générale, les instruments d'optique. Ceux-ci sont constitués d'objets réfractant qui ont nécessairement au moins 2 faces. Schématiquement, on peut considérer l'association de deux dioptres plans non parallèles : on a alors un prisme, dont les propriétés de réfexion totale ou de dispersion en font un objet largement utilisé. Et considérer par ailleurs l'association de 2 dioptres dont l'un (au moins) n'est pas plan : les lentilles, pour lesquelles on retrouve naturellement les conditions de Gauss pour pouvoir associer une image à un objet.

















































