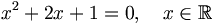Équation - Définition
En mathématiques, une équation est une égalité qui lie différentes quantités, généralement pour poser le problème de leur identité. Résoudre l'équation consiste à déterminer toutes les façons de donner à certaines des quantités qui y apparaissent, les inconnues, des valeurs qui rendent l'énoncé vrai. Ces valeurs possibles sont appelées solutions de l'équation. Une équation est souvent utilisée pour faire référence à l'ensemble de ses solutions, et en géométrie notamment, on appelle équation d'un objet mathématique sa définition comme ensemble des solutions d'une équation. Dans un sens plus large, le terme équation est synonyme d'égalité, avec fréquemment le sous-entendu que l'égalité n'est pas toujours vraie.
Une équation se présente le plus souvent comme une formule du type A = B. (Cependant, n'importe quel problème mathématique peut être vu comme une équation, sans toujours être exprimé explicitement sous cette forme.) Les deux membres A et B séparés par le signe = dépendent de variables (inconnues ou paramètres) dont les valeurs ne sont pas spécifiées. On y ajoute, parfois implicitement, la donnée des ensembles où l'on cherche des valeurs pour les inconnues. Par exemple, l'équation
d'inconnue x admet pour unique solution le réel − 1.
On réserve des noms particuliers à certains types d'équations. Ainsi, lorsqu'elle est écrite comme la " combinaison " de plusieurs équations plus simples qui doivent être vérifiées simultanément, on parle de système d'équations ou simplement de système.
Certaines informations nécessaires à la compréhension et la résolution d'une équation sont parfois sous-entendues. En particulier, une convention usuelle de notation veut que les lettres du début de l'alphabet (a, b, A, B...) représentent des paramètres, alors que celles de la fin de l'alphabet (principalement x, y, z, X) désignent des inconnues. Ainsi " Résoudre l'équation ax2 + bx + c = 0, d'inconnue
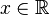
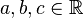

Certaines catégories d'équations font l'objet de théories générales. On parvient ainsi à résoudre certaines classes d'équations en exprimant leurs solutions sous une forme plus explicite que l'équation elle-même. Dans les cas moins favorables, on se contente d'étudier les conditions d'existence des solutions et leurs propriétés.
Propriétés
Si une équation algébrique est vraie, alors les opérations suivantes peuvent y être appliquées et la nouvelle équation sera encore vraie :
- N'importe quelle quantité peut être additionnée de chaque côté de l'égalité.
- N'importe quelle quantité peut être soustraite de chaque côté de l'égalité.
- N'importe quelle quantité peut multiplier chaque côté de l'égalité.
- N'importe quelle quantité différente de zéro peut diviser chaque côté de l'égalité.
- Généralement, n'importe quelle fonction peut être appliquée de chaque côté de l'égalité. Cependant, le nombre de solutions peut changer, ce qui peut ne pas être souhaité.
Les propriétés algébriques (1-4) impliquent que l'égalité est une relation de congruence dans un corps. En pratique, c'est la seule. L'ensemble des nombres réels, étant un corps, permet ces transformations. Cependant, si l'équation de départ est valide dans l'ensemble des nombres naturels, la division et la soustraction ne permettent pas de maintenir la véracité de la nouvelle équation.
Les fonctions 1 à 4 étant injectives (sauf en multipliant par 0 des deux côtés de l'équation pour 3.), elles ne modifient pas le nombre de solutions. Si une fonction non injective est appliquée aux deux côtés d'une équation vraie, alors l'équation résultante peut encore être vraie, mais elle sera moins utile. Formellement, il s'agit d'une implication logique, pas d'une équivalence, ce qui peut mener à agrandir l'ensemble solution.
Types
À cause de leur importance relative, certaines équations sont regroupées dans des classes à part :
- équation linéaire
- équation polynomiale
- équation différentielle
- équation aux dérivées partielles.
Paramétrique
Une équation paramétrique se présente sous la forme
-
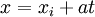
-
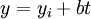
-
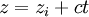
-
laquelle représente un object algébrique dépendant du paramètre
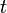
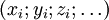
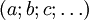
Supposons qu'une droite
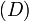
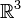
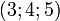
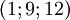
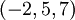
-
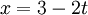
-
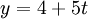
-
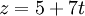
Symétrique
Une équation symétrique se présente sous la forme
-
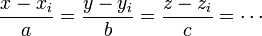
laquelle représente un object algébrique passant par le point
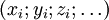
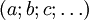
Supposons qu'une droite
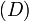
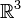
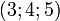
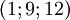
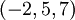
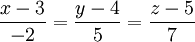
Vectorielle
Une équation vectorielle fait intervenir à la fois des vecteurs et des scalaires :
-
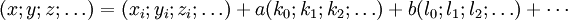
laquelle représente un object algébrique passant par le point
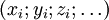
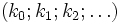
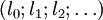
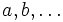
Supposons qu'un objet
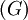
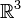
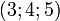
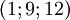
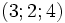
-
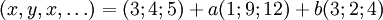
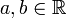
Puisque les deux vecteurs ne sont ni parallèles (l'un n'est pas multiple de l'autre) ni orthogonaux (le produit scalaire des deux n'est pas nul), alors