Indice de pouvoir de Banzhaf - Définition

Histoire

Ce qui est connu aujourd'hui comme l'indice de pouvoir de Banzhaf a été initialement présenté par Penrose en 1946 et fut en grande partie oublié par la suite. Il a été réinventée par Banzhaf en 1965, mais il dû être réinventer une fois de plus par Coleman en 1971 avant qu'il soit incorporé à la littérature traditionnelle.

Banzhaf voulait prouver objectivement que le système de vote au Conseil du Comté de Nassau était injuste. Comme cela est indiqué dans Game Theory and Strategy, les votes étaient répartis comme suit :

• Hempstead 1: 9
• Hempstead 2: 9
• North Hempstead: 7
• Oyster Bay: 3
• Glen Cove: 1
• Long Beach: 1

On a au total 30 voix, et une majorité simple de 16 voix était nécessaire pour qu'une mesure puisse passer.
En utilisant la notation de Banzhaf, [Hempstead 1, Hempstead 2, North Hempstead, Oyster Bay, Glen Cove, Long Beach] sont notés de A à F et on a le système de poids suivant :
[16, 9, 9, 7, 3, 1, 1]

Il y a 32 coalitions gagnantes, et 48 votes décisifs :
AB, AC, BC, ABC, ABD, ABE, ABF, ACD, ACE, ACF, BCD, BCE, BCF, ABCD, ABCE, ABCF, ABDE, ABDF, ABEF, ACDE, ACDF, ACEF, BCDE, BCDF, BCEF, ABCDE, ABCDF, ABCEF, ABDEF, ACDEF, BCDEF et ABCDEF

L'indice de Banzhaf donne les valeurs de pouvoirs suivantes :

• Hempstead 1 = 16/48
• Hempstead 2 = 16/48
• North Hempstead = 16/48
• Oyster Bay = 0 / 48
• Glen Cove = 0 / 48
• Long Beach = 0 / 48

Banzhaf a fait valoir qu'une convention de vote qui donne 0% du pouvoir à 16% de la population est injuste, et a poursuivi le Conseil en Justice.
Aujourd'hui, l'indice de pouvoir de Banzhaf est un moyen accepté pour mesurer le pouvoir d’un vote, en alternance avec l’indice de pouvoir de Shapley-Shubik. Cependant, l'analyse de Banzhaf a été critiquée pour traiter les voix, comme des pièces de monnaie se retournant, et un modèle empirique de vote plutôt qu’un modèle de vote aléatoire tel qu'il est utilisé par Banzhaf apporte des résultats différents (Gelman & Katz 2002).

Écriture mathématique

Indice de Banzhaf : Pour un jeu (N,v) l'indice de Banzhaf du joueur i est :

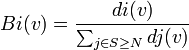
où di(v) est l'ensemble des coalitions pour lesquelles i est décisif.