Théorème de factorisation (de morphismes) - Définition
Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
La liste des auteurs de cet article est disponible ici.
Le cas des espaces vectoriels
On considère un espace vectoriel E et la relation d'équivalence définie par un sous-espace vectoriel H: xRx' si
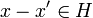
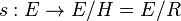
Théorème — Soit
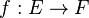
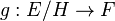
- g est surjective si f est surjective;
- g est injective si on a H = Kerf;
- g est un isomorphisme si f est surjectif et H = Kerf.

















































