Théorème des quatre carrés de Lagrange - Définition
Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
La liste des auteurs de cet article est disponible ici.
Fonctions arithmétiques
Les fonctions arithmétiques permettent d'obtenir des résultats plus généraux. Si on pose r4(n) comme étant le nombre de façon de décomposer n sous forme d'une somme de 4 carrés, on obtient le résultat suivant:
-
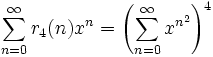
Moyennant l'utilisation des séries de Lambert, on en déduit le théorème suivant, dit théorème de Jacobi :
![\forall n \in \mathbb{N}^*, \ r_4(n) = 8 \sum_{d|n, d \not\equiv 0[4]}{d}](https://static.techno-science.net/illustrationWebp/Definitions/autres/f/f2de8fa897b940dd87bfb7457bc12e72_b5eb3a221acd7bcea8fbf7fdf9fd486a.png)
Par exemple, 1 n'est divisible que par lui-même, qui n'est pas congru à 0 modulo 4. Donc r4(1) = 8
3 des 8 formes sont :
1 = 12 + 02 + 02 + 02
1 = 02 + 12 + 02 + 02
1 = ( − 1)2 + 02 + 02 + 02
