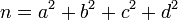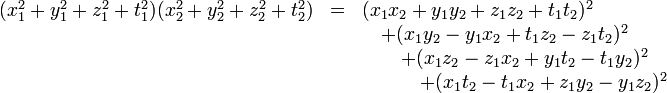Théorème des quatre carrés de Lagrange - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Le théorème des quatre carrés de Lagrange, aussi connu sous le nom de conjecture de Bachet et démontré en 1770 par le mathématicien français Joseph Louis Lagrange correspond à une équation diophantienne qui se résout avec les techniques de l'arithmétique modulaire. Il s'énonce de la façon suivante :
- Tout entier positif peut s'exprimer comme la somme d'au plus quatre carrés.
Plus formellement, pour tout entier positif n, il existe des entiers positifs a, b, c, d tels que :
Le mathématicien français Adrien-Marie Legendre améliora le théorème en 1798 en affirmant qu'un entier positif peut être exprimé comme la somme d'au plus trois carrés si et seulement s'il n'est pas de la forme
-
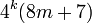
Sa démonstration était incomplète, laissant une brèche qui fut comblée plus tard par le mathématicien allemand Carl Friedrich Gauss.
Le théorème des quatre carrés de Lagrange est un cas particulier du théorème du nombre polygonal de Fermat (en) et du problème de Waring.
La démonstration du théorème repose (en partie) sur l'identité des quatre carrés d'Euler :
Démonstration basée sur les quaternions d'Hurwitz
Nous allons travailler sur l'ensemble des quaternions d'Hurwitz, également appelés entiers d'Hurwitz, qui sont des quaternions particuliers.
Quelques propriétés
Les entiers d’Hurwitz
Les entiers d’Hurwitz sont les nombres de la forme : a.(1 + i + j + k) / 2 + b.i + c.j + d.k avec
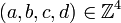
![\mathbb{Z} [h,i,j,k]](https://static.techno-science.net/illustration/Definitions/autres/8/840ef30ae2eae5cbde635ada3b76039c_0857e052c48067798de282ec5b414486.png)
On a alors la somme et le produit des deux entiers d’Hurwitz est un entier d’Hurwitz (les entiers d'Hurwitz forment un sous anneau de l'anneau formé par l'ensemble des quaternions, l'addition et la multiplication usuelles).
On rappelle que la norme d’un quaternion (et donc d’un entier d’Hurwitz) de la forme α = a + b.i + c.j + d.k est
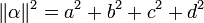
Il existe donc 24 nombres unités : 8 formés par
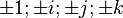
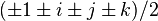
Identité des quatre carrés d’Euler
On démontre que si deux nombres s’écrivent sous forme de somme de quatre carrés, alors leur produit s’écrit aussi sous forme de somme de quatre carrés. On peut le démontrer, soit à partir de l’identité des quatre carrés d’Euler, soit en écrivant que la norme d’un produit est le produit des normes.
Division
Les entiers d’Hurwitz obéissent à la propriété de la division selon laquelle, de la même manière qu’avec la division euclidienne :
Si a et b sont des entiers d’Hurwitz, b non nul, il existe un quotient q et un reste r tel que :
a=b.q+r avec
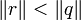
Les quaternions d'Hurwitz forment donc un anneau euclidien à gauche et à droite.
Par exemple :
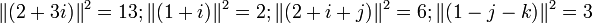
Comme 2 + 3i = (1 + i).(2 + i + j) + (1 − j − k),
2+3i divisé par 1+i admet comme couple (quotient,reste) le couple (2+i+j,1-j-k) Ce couple n’est pas unique puisque cette division admet aussi le couple (2+i+k,1+j-k)
On dira que a divise b (ou que a admet comme diviseur b) s’il existe q tel que a = b.q. q est alors unique.
Entier d’Hurwitz premier
Un entier d’Hurwitz p est premier s’il n’admet comme diviseur que les nombre unités et p fois les nombres unités.
Or, si a divise b,
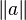
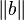
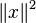
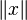
1+i est, par exemple, un entier d’Hurwitz premier, car
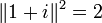
Algorithme d’Euclide
On peut définir un algorithme d’Euclide dans
![\mathbb{Z} [h,i,j,k]](https://static.techno-science.net/illustration/Definitions/autres/8/840ef30ae2eae5cbde635ada3b76039c_0857e052c48067798de282ec5b414486.png)

On peut ainsi trouver un plus grand diviseur commun à a et b (noté pgcd(a ,b)), c'est-à-dire celui ayant la plus grande norme. En toute rigueur, étant donné la non commutativité de cet ensemble, on doit définir un plus grand diviseur commun à droite, et un plus grand diviseur commun à gauche.
De même que dans

Propriété de la division d’un produit par un entier réel d’Hurwitz premier
Si p est un entier réel d’Hurwitz premier (c'est-à-dire un nombre premier appartenant à

Preuve
Supposons que p premier divise a.b mais ne divise pas a. Alors, un pgcd de a et p est 1, et il existe u et v tels que au+pv=1.
Alors en multipliant par b de chaque coté, on obtient bau+bpv=b. p divise ab donc bau, et p divise p donc bpv (comme p appartient à

Donc p divise b.
Théorème et lemme préliminaires
Tout d’abord, remarquons que 0, 1 et 2 peuvent s’écrire sous forme de somme de 4 carrés (0 = 02 + 02 + 02 + 02;1 = 12 + 02 + 02 + 02 et 2 = 12 + 12 + 02 + 02).
Théorème
Tout entier premier de

Preuve
Soit p remplissant les conditions précédentes. On peut donc écrire p sous la forme p = (a + bi + cj + dk)γ , avec
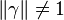
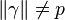
On a alors le conjugué de p (égal à p puisque p appartient à

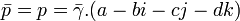
Alors
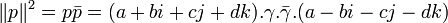
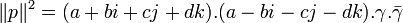
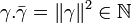
Donc
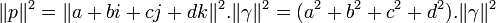
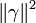
Étant donné que p est premier, la seule décomposition de p2 est donc p.p. On en déduit que (a2 + b2 + c2 + d2) = p.
Si a, b, c et d sont des entiers, p s’écrit comme somme de quatre carrés.
Si ce sont des demis-entiers, on peut alors trouver w tel que :
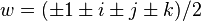
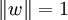
On a alors :
p = (a + bi + cj + dk)(a − bi − cj − dk)
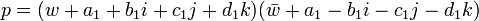
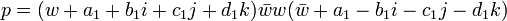
Or comme a1,b1,c1 et d1 sont des entiers pairs,
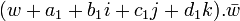
Donc p s’écrit comme somme de quatre carrés.
Lemme
Soit p un entier premier impair, alors il existe l et m tels que p divise 1 + l2 + m2 (p, l et m appartenant à

Preuve
Soit p premier impair. Les différentes classes de congruence modulo p sont 0, 1, -1, ..., (p-1)/2, -(p-1)/2. Il y en a donc p.
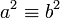


De même pour − 1 − m2, il y a (p + 1) / 2 éléments qui sont de cette forme, différents, modulo p. Supposons que ces deux ensembles soient disjoints. Alors il y aurait (p + 1) / 2 + (p + 1) / 2 = p + 1 éléments dans
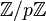
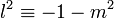
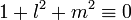
Il existe donc l et m tel que p divise 1 + l2 + m2.
Théorème des quatre carrés
Tout entier de

Preuve
Soit p un entier impair premier. Il existe donc d’après le lemme précédant l et m entier tel que p divise 1 + l2 + m2. Donc p divise 1 + l2 + m2 = (1 + li + mj)(1 − li − mj).
Supposons que p soit un entier d’Hurwitz premier. Alors d’après un théorème précédant, p divise 1 + li + mj ou p divise 1 − li − mj. Or, ni
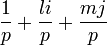
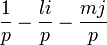
D’après le théorème précédant, p peut donc s’écrire sous forme de somme de quatre carrés.
Donc, si p est un entier impair premier, p peut donc s’écrire sous forme de somme de quatre carrés.
Si p=0, p=1 ou p=2, nous avons déjà vu que p peut s’écrire sous forme de somme de quatre carrés.
Si p est un entier, non premier, strictement supérieur à 2, alors p peut s’écrire sous forme de produit de nombre premiers. Ces nombres premiers peuvent s’écrire sous forme de carrés, et leur produits aussi, d’après la remarque sur l’identité des quatre carrés d’Euler. Donc p peut s’écrire sous forme de somme de quatre carrés.
Finalement, tout élément de