Inversion (géométrie) - Définition

Propriétés

• Une inversion de rapport non-nul est bijective.
• Une inversion est une involution : elle est sa propre réciproque.
• On appelle sphère d’inversion (ou cercle d’inversion dans le plan) la sphère de centre et de rayon . Elle est toujours globalement invariante, et elle est invariante point par point lorsque le rapport est positif.
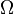
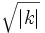
• Les hyperplans passant par sont aussi des invariants globaux.

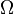
Le principal intérêt des inversions est la propriété de conservation hyperplans/hypersphères (ou des droites/cercles dans le plan) :

Théorème

L’ensemble constitué par les hypersphères et les hyperplans est stable par inversion. Autrement dit, l’image, par une inversion, d’une hypersphère ou d’un hyperplan, est une hypersphère ou un hyperplan. Mais il est parfaitement possible que l’image d’une hypersphère (resp. d’un hyperplan) soit un hyperplan (resp. une hypersphère).