Inversion (géométrie) - Définition
La liste des auteurs de cet article est disponible ici.
Définition générale dans le cadre d’un espace affine euclidien
Soit
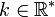
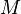
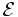
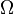
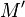
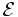
-
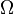
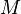
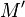
-

On peut ainsi définir l’inversion de centre
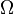
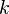
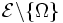
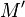
- Analyse
- Supposons qu’un tel point
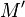
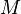
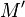
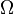

- Et comme
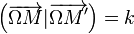
-
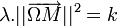
- Puisque
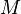
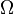
-

- Synthèse
- Le point

- Remarque
- Pourquoi n’avons nous pas simplement défini une inversion à partir de la formule précédente ? Parce qu’en fait la définition reste valable dans un espace affine quelconque, dès lors que l’on dispose d’une valeur algébrique sur les droites...
Dans le plan
Dans le plan affine euclidien
Dans le plan affine euclidien, l’inverse d’un point est constructible au compas lorsqu’on connait le , ce qui permet de démontrer le :
- Théorème de Mohr et Mascheroni
- Toute construction à la règle et au compas peut se faire uniquement au compas (à l’exception des tracés des portions de droites).
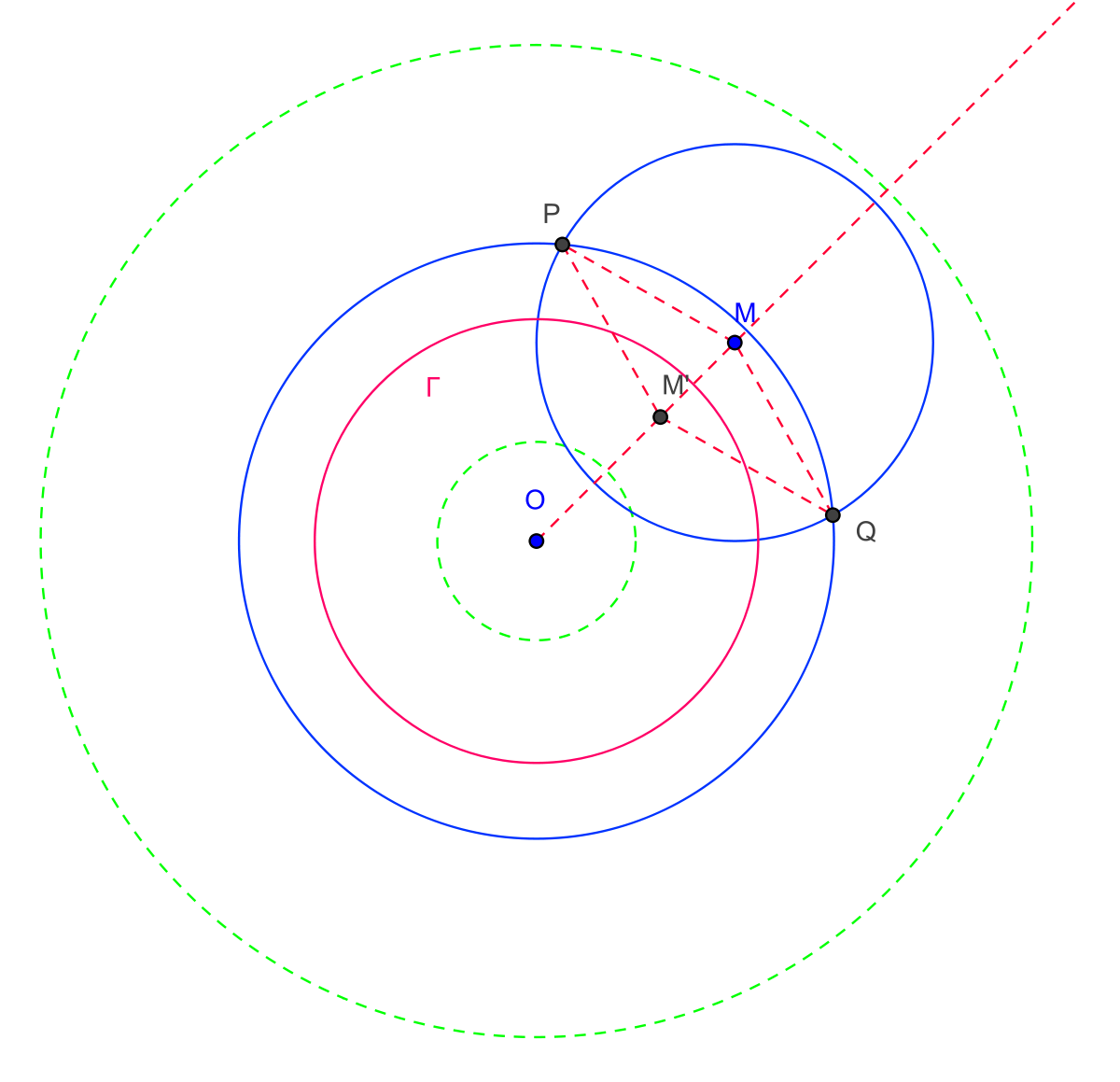
Signalons aussi l’existence de "machines à inversion", l’inverseur de Charles Peaucellier :
L'inverseur est un objet mécanique avec deux barres OP et OQ de longueur fixe


- Pour un point

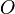
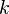
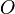


- Un point
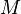
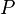
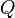
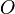

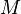

- Puis on construit l’unique point
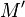

- L’application qui à
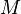
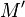
- Un point
Remarque : cet inverseur fut utilisé pour transformer un mouvement rectiligne en mouvement circulaire.
Voir : figure interactive de ChronoMath
Dans le plan complexe
Dans le plan complexe, une inversion particulière est celle par rapport au cercle unité ; en termes d’affixe complexe, elle est codée par l'application

C’est en fait un résultat général : un cercle d’inversion étant donné, on choisit trois points



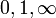



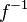
On fait ensuite le lien avec le groupe circulaire, qui est l’ensemble des transformations, définies en fait sur la droite projective complexe, et qui envoient les droites et les cercles sur des droites et des cercles ; en identifiant la droite projective complexe à la sphère de Riemann, cette propriété de conservation s’exprime plus simplement : ce sont les cercles tracés sur cette sphère qui sont conservés. Il est clair que les inversions appartiennent au groupe circulaire ; et relativement simple de montrer qu’il en est de même pour les homographies. On peut montrer ensuite qu’en fait, le groupe circulaire est engendré par inversions et homographies.