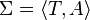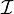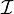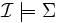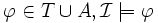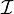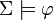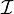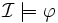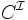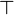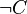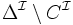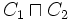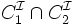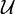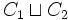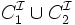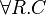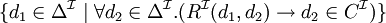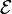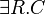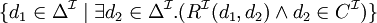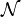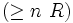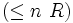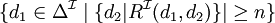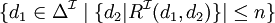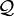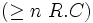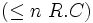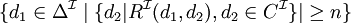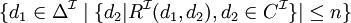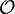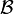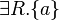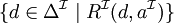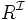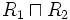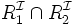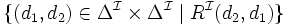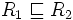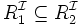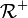Logique de description - Définition
La liste des auteurs de cet article est disponible ici.
Définition des logiques de description
La plupart des logiques de description divisent la connaissance en deux parties :
- les informations terminologiques: définition des notions basiques ou dérivées et de comment elles sont reliées entre elles. Ces informations sont "génériques" ou "globales", vraies dans tous les modèles et pour tous les individus.
- les informations sur les individus: ces informations sont "spécifiques" ou "locales", vraies pour certains individus particuliers.
Toutes les informations connues sont alors modélisées comme un couple
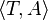
Une autre manière de voir la séparation entre ces informations, est d'associer la T-Box aux règles qui régissent notre monde (e.g., la physique, la chimie, la biologie, ...), et d'associer les individus de notre monde à la A-Box (e.g., Jean, Marie, un chat, ...).
La sémantique
Les logiques de description utilisent les notions de concept, de rôle et d'individu. Les concepts correspondent à des "classes d'éléments" et sont interprétés comme un ensemble dans un univers donné. Les rôles correspondent aux "liens entre les éléments" et sont interprétés comme des relations binaires sur un univers donné. Les individus correspondent aux éléments d'un univers donné. La sémantique des logiques de description est définie comme suit :
Définition 1 :
- Soit
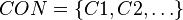
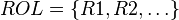
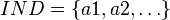
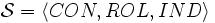
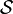
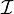
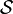
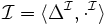
-
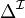
-
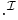
- un élément
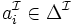
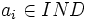
- un sous-ensemble
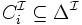
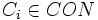
- et une relation
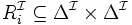
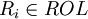
- un élément
-
En d'autres mots, une interprétation de la logique de description n'est rien de plus qu'un modèle pour un type particulier de signature du première ordre, où seulement les prédicats unaires et binaires sont autorisés et l'ensemble des symboles de fonctions est vide.
La base de connaissance
Typiquement, la base de connaissance standard utilisée par les logiques de description est définie de la manière suivante :
Définition 2 :
- Étant donné un langage de description
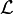
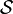
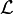
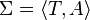
- T est la T(erminologique)-Box, un ensemble fini, qui peut être vide, d'expressions appelées GCI (General Concept Inclusion) de la forme
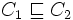
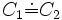
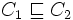
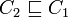
- A est la A(ssertion)-Box, un ensemble fini, qui peut être vide, d'expressions de la forme a:C ou (a,b):R où C est un concept sans restriction, R un rôle qui n'est pas forcément atomique et a,b appartiennent à IND. Les formules de A sont appelées des assertions.
- T est la T(erminologique)-Box, un ensemble fini, qui peut être vide, d'expressions appelées GCI (General Concept Inclusion) de la forme
Les axiomes terminologiques ont été pensés à l'origine comme une définition, et nombre de conditions plus restrictives ont été imposées. Les deux restrictions les plus importantes sont les suivantes :
- axiome terminological simple : dans tous les axiomes terminologiques
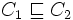
- définition acyclique : le graphe obtenu en assignat un nœud nA à chaque concept atomique A de la T-Box, et un arc orienté entre deux nœuds nA et nB s'il existe un axiome terminologique
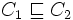
Ces restrictions sont liées à l'idée de considérer les axiomes terminologiques comme des définitions de concepts.
Les différentes logiques de description
Les logiques de descriptions ont une base commune enrichie de différentes extensions (voir tableau ci-dessous). On peut dès lors avoir des concepts complexes composés de concepts atomiques, et de même pour les rôles.
| Lettre | Constructeur | Syntaxe | Sémantique |
|---|---|---|---|
|
| nom de concept | C |
|
|
| top |
|
|
|
| négation de concepts non nécessairement primitifs |
|
|
|
| conjonction |
|
|
|
| disjonction |
|
|
|
| quantificateur universel |
|
|
|
| quantificateur existentiel typé |
|
|
|
| restriction de nombre |
|
|
|
| restriction de nombre qualifiée |
|
|
|
| un-de |
|
|
|
| role filler |
|
|
|
| nom de rôle | R |
|
|
| conjonction de rôles |
|
|
|
| rôles inverses | R − 1 |
|
|
| hiérarchie des rôles |
|
|
|
| transitivité des rôles | R + | Plus petite relation transitive contenant
|
L'une des premières logiques de description est le langage
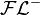
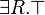
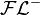
La logique
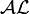
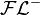
Les logiques de description qui existent sont des combinaisons des différents éléments du tableau ci-dessus. Par exemple, si on rajoute la négation complète
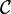
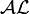
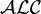
Certaines logiques sont équivalentes, notamment
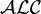
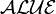
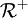
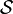
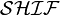
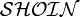
Inférences
En LD, la notion d'inférence est décrite comme ci-dessous:
Définition 3 :
- Soit
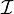

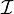

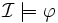
-
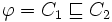
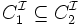
-
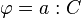
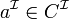
-
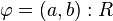
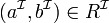
-
Soit