Loi de composition interne - Définition
La liste des auteurs de cet article est disponible ici.
Propriétés
Certaines propriétés des lois de composition interne, particulièrement intéressantes, ont reçu un nom. Soit un magma ( E,


Existence d’éléments remarquables
-


-
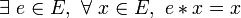
- Une loi peut présenter plusieurs éléments neutres à gauche, à condition qu’elle ne présente pas d’élément neutre à droite;
-


-
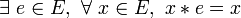
- Une loi peut présenter plusieurs éléments neutres à droite, à condition qu’elle ne présente pas d’élément neutre à gauche;
-


-
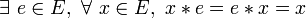
- Une loi est unifère si et seulement si elle est unifère à gauche et unifère à droite;
- L’élément neutre d’une loi unifère est unique;
-


-
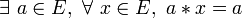
- Une loi peut présenter plusieurs éléments absorbants à gauche, à condition qu’elle ne présente pas d’élément absorbant à droite;
-


-
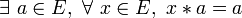
- Une loi peut présenter plusieurs éléments absorbants à droite, à condition qu’elle ne présente pas d’élément absorbant à gauche;
-


-
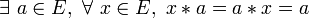
- Une loi est absorbante si et seulement si elle est absorbante à gauche et absorbante à droite;
- L’élément absorbant d’une loi absorbante est unique;
-

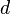
-
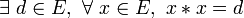
- L’élément dévolutif d’une loi dévolutive est unique;
-

-
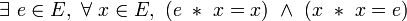
- Une loi est involutive à gauche si et seulement si elle est unifère à gauche et dévolutive, et l’élément neutre à gauche est l’élément dévolutif.
-

-
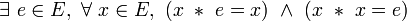
- Une loi est involutive à droite si et seulement si elle est unifère à droite et dévolutive, et l’élément neutre à droite est l’élément dévolutif.
-

-
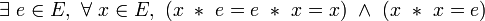
- Une loi est involutive si et seulement si elle est unifère et dévolutive, et l’élément neutre est l’élément dévolutif.
-

-
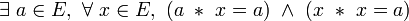
- Une loi est nilpotente à gauche si et seulement si elle est absorbante à gauche et dévolutive, et l’élément absorbant à gauche est l’élément dévolutif.
-

-
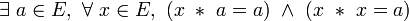
- Une loi est nilpotente à droite si et seulement si elle est absorbante à droite et dévolutive, et l’élément absorbant à droite est l’élément dévolutif.
-

-
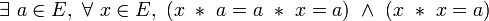
- Une loi est nilpotente si et seulement si elle est absorbante et dévolutive, et l’élément absorbant est l’élément dévolutif.
Régularité et propriétés liées
-

-

-

-
![\forall\ ( x , y , z ) \in E^3 ,\ [\ ( x * y = x * z ) \or ( y * x = z * x )\ ] \Rightarrow ( y = z ) \,](https://static.techno-science.net/illustration/Definitions/autres/9/9ed02e073a2234a03f483f19f7b9393d_2aa1c88204a0005b8938db3cbbe5e928.png)
- Une loi est régulière si et seulement si elle est régulière à gauche et régulière à droite.
-

-



-
![\forall\ ( a , b ) \in E^2 , [\ \exists\ x \in E /\ ( a * x = b ) \wedge [\ \forall\ z \in E ,\ ( a * z = b ) \Rightarrow ( z = x ) ] ] \,](https://static.techno-science.net/illustration/Definitions/autres/4/46c4653a7e1f760acbec44a4fc774edf_964428e6a66da291b3468bdfe111335b.png)
-
- Cette propriété est plus forte que la régularité : une loi symogène est nécessairement régulière. Toutefois, dans le cas d'un magma fini, symogénéité et régularité sont équivalentes.
Associativité et propriétés analogues
-

-
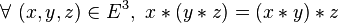
- On peut noter que l’associativité d’une loi permet de se passer des parenthèses quand on répète la loi; la plupart des lois intéressantes sont associatives (exemples : l’addition, la multiplication, la composition des correspondances,...).
-

-
![\forall\ ( x , y ) \in E^2 ,\ [\ x * ( x * y ) = ( x * x ) * y \ ] \wedge [\ ( x * y ) * y = x * ( y * y )\ ] \,](https://static.techno-science.net/illustration/Definitions/autres/4/431b392eef9f32a1027086554df87af5_101eeccbb363294087783992fe6f9036.png)
- Cette propriété est moins forte que l'associativité, puisqu’une loi associative est nécessairement alternative.
-

-
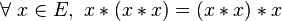
- Cette propriété est moins forte que l’alternativité, puisqu’une loi alternative est nécessairement associative des puissances.
- Quand cette propriété est vérifiée, il est possible d’introduire la notion de puissance d’un élément (d’où le nom de la propriété) :
- - la puissance n-ième d’un élément x, notée habituellement « x n », est égale au résultat de la composition de x selon




- - si, de plus, la loi

- - si, de plus, la loi

- - la puissance n-ième d’un élément x, notée habituellement « x n », est égale au résultat de la composition de x selon
-

-
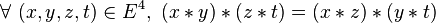
- Cette propriété est appelée permutativité car elle permet de permuter les termes moyens dans les expressions du type ci-dessus.
- Cette propriété est moins forte que l’associativité, car une loi associative et commutative est nécessairement permutative; notons toutefois qu’une loi associative, mais non-commutative, n’est pas nécessairement permutative, et qu’une loi permutative, même commutative, n’est pas nécessairement associative.
- (Exemples de lois permutatives non associatives : la soustraction dans
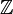
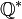
-

-
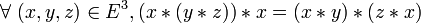
- Cette propriété est moins forte que l’associativité, puisqu'une loi associative est nécessairement neutroactive.
Autres propriétés
-

-

-

-
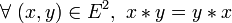
- Les lois commutatives sont notées par « + », «
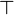


- Les notions de permutativité et de commutativité sont des notions différentes: il existe des lois permutatives et non commutatives (comme la soustraction dans
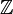
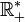
La liste de propriétés ci-dessus n’est pas exhaustive, loin de là. Toutefois, nous n'aborderons dans ce paragraphe qu’un seul autre cas : dans des structures algébriques comportant plusieurs lois, certaines de ces lois ont des propriétés relatives à d’autres lois. La plus importante de ces lois relatives est la distributivité.
- Une loi


Cette propriété se décompose en deux parties :
- - distributivité à gauche :
-
- - distributivité à droite :
-
Remarque : si dans la situation ci-dessus la loi


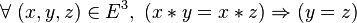
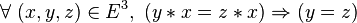
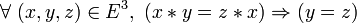
![\wedge [\ \exists\ y \in E /\ ( y * a = b ) \wedge [\ \forall\ z \in E ,\ ( z * a = b ) \Rightarrow ( z = y )\ ] ] \,](https://static.techno-science.net/illustration/Definitions/autres/6/6dd3b8f08f572a8ba62cd5ea8fbfa3f7_811d410a4b55bf66bbd5c4423ee295af.png)
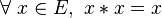
![\exists\ a \in E ,\ \forall\ x \in E ,\ ( x\ *\ a = a\ *\ x = a )\ \wedge\ [\ \forall\ y \in E ,\ ( x\ *\ y = a ) \Rightarrow [\ ( x = a )\ \vee\ ( y = a ) \ ]\ ] \,](https://static.techno-science.net/illustration/Definitions/autres/9/98f651877534c036de40ccafd7275ece_4dbf867757d43767af3ce0f495cf0006.png)
![\forall\ ( x , y , z , t ) \in E^4 ,\ ( x \bot y ) * ( z \bot t ) = [ ( x * z ) \bot ( x * t ) ]\ \bot\ [ ( y * z ) \bot (y * t ) ] \,](https://static.techno-science.net/illustration/Definitions/autres/4/4f1a20433cfa3a425732ea0050a34e16_9f495b81e666d823077727b1750bf0a7.png)