Loi de composition interne - Définition

Introduction

L’algèbre est la branche des mathématiques qui s’intéresse aux ensembles et aux relations qui peuvent y être établies. Elle recherche les conséquences générales qui découlent des propriétés de ces relations, indépendamment de la nature précise des ensembles et des relations en cause. Parmi les relations étudiées, les lois de composition interne occupent une place privilégiée.

Présentation

Nous avons tous depuis le primaire une assez bonne idée de la notion d'opérations telles que l'addition, la soustraction, la multiplication ou la division. Une opération (interne) dans un ensemble est une relation interne dans cet ensemble, qui, à deux éléments quelconques de cet ensemble, appelés opérandes, en associe éventuellement un troisième, unique, nommé résultat, toujours dans ce même ensemble.

Pour que l’opération considérée soit effectivement une loi de composition interne, il faut qu’elle ait un sens quels que soient les deux éléments de l’ensemble choisis (on dit formellement que l'opération doit être définie partout). Ainsi :

• la division n’est pas une loi de composition interne dans , parce qu’on ne peut pas diviser par zéro : par exemple, « 3 / 0 » n’a pas de sens. Mais cette même division est une loi de composition interne dans (ensemble des réels privés de 0). Enfin cette même opération n'est pas une loi de composition interne dans car 2 / 3 n'est pas un entier relatif.
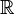
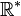
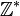
• la soustraction peut être ou non une loi de composition interne selon l’ensemble de nombres considéré :
  • s’il s’agit de l’ensemble des nombres usuels, dits entiers naturels { 0, 1, 2, 3,... }, ce n’en est pas une, puisque « 3 - 5 », par exemple, n’a pas pour résultat l’un de ces nombres usuels.
  • si au contraire, on choisit l’ensemble des entiers relatifs, qui en plus des entiers naturels, contient les entiers négatifs { ..., -3, -2, -1}, alors la soustraction est bien une loi de composition interne.

En résumé, une loi de composition interne dans un ensemble E, ou, plus simplement une loi dans E, est une opération qui donne un résultat dans E pour tous les couples possibles d'éléments de E.

Définition formelle

On appelle loi de composition interne sur un ensemble E toute application de E × E dans E.

Un ensemble E muni d’une loi de composition interne constitue une structure algébrique appelée magma et notée « ( E, ) ».

Quelques exemples triviaux, pour un ensemble E non vide :

• les applications constantes : si c appartient à E : x E, y E,   x y   = c ;
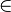
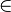
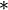
• l’application sélectionnant le terme de gauche : x E, y E,   x y   = x ;
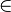
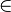
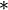
• l’application sélectionnant le terme de droite : x E, y E,   x y   = y.

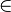
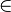
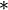
Exemple

Dans l’ensemble des entiers relatifs, l’addition est une loi de composition interne ayant entre autres les propriétés suivantes, qui seront définies plus formellement dans la seconde partie de l’article :

• zéro est élément neutre pour cette loi : l’ajouter à n’importe quel nombre redonne ce nombre : par exemple,   5 + 0 = 5  , et   0 + 8 = 8   ;
• pour tout entier, il existe un autre nombre, son opposé (le terme général est élément symétrique), tel qu’ajouté au premier, il redonne l’élément neutre, zéro. L’opposé se note comme l’entier initial changé de signe. Ainsi :   3 + (-3) = 0   ;
• on peut échanger les deux éléments autour du signe «  +  » :   3 + 5 = 5 + 3 = 8   . On dit que l’opération est commutative ;
• on peut grouper les éléments comme on le souhaite quand on en ajoute plus de deux :   3 + 5 + 4   peut se calculer de deux manières :
  • en calculant d’abord   3 + 5 = 8   puis en ajoutant   4   au résultat,
  • ou en calculant   5 + 4 = 9   avant de calculer   3 + 9   .

Ces deux méthodes mènent au même résultat, ce que l’on note :   (3 + 5) + 4 = 3 + (5 + 4)   . On dit que l’opération est associative.

Ces quatre propriétés, existence d’un élément neutre, existence de symétriques, commutativité, associativité, peuvent se retrouver pour d’autres ensembles et d’autres lois. Ainsi, on peut étudier l’ensemble des translations (c’est-à-dire les déplacements en ligne droite : par exemple, se déplacer de 3 mètres vers la gauche et de 2 mètres vers le haut), et une loi de composition interne sur cet ensemble, la composition : la composition de deux translations consistant simplement à faire le premier déplacement, puis le second. On retrouve pour la composition les mêmes propriétés que pour l’addition :

• le neutre est la translation nulle, consistant à ne pas se déplacer ;
• le symétrique d’une translation consiste à faire le même déplacement dans l’autre sens (3 mètres à droite et 2 mètres vers le bas pour l’exemple précédent) : si on fait successivement les deux, c’est comme si on faisait le déplacement nul ;
• on peut faire les déplacements dans l’ordre qu’on veut, on retrouve la commutativité et l’associativité.

L’ensemble des entiers relatifs avec l’addition, et l’ensemble des translations avec la composition ont ces propriétés simples en commun. Un ensemble et une loi qui possèdent ces quatre propriétés particulières s’appelle en algèbre un groupe abélien. L’algèbre s’attache ensuite à rechercher d’autres propriétés plus complexes qui découlent de ces quatre premières. Ces nouvelles propriétés seront alors valables aussi bien pour l’ensemble des entiers relatifs que pour celui des translations, et pour tout autre ensemble et tout autre loi de composition interne ayant la structure d’un groupe abélien, sans qu’il soit nécessaire de le redémontrer pour chacun.