Loi de composition interne - Définition

Inversibilité

Cette propriété importante mérite un paragraphe séparé. Nous nous placerons dans un magma ( E, ) dont nous supposerons la loi unifère, c'est-à-dire disposant d'un élément neutre . Il est alors possible de définir les notions suivantes:

• un élément est dit symétrisable à gauche ou inversible à gauche si :

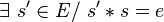
s' est alors appelé élément symétrique à gauche de s;

• un élément est dit symétrisable à droite ou inversible à droite si :

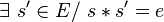
s' est alors appelé élément symétrique à droite de s;

• un élément est dit symétrisable ou inversible lorsqu'il est inversible à droite et à gauche et que les deux symétriques sont égaux;

s' est alors appelé élément symétrique de s.

Note : attention à ne pas confondre le symétrique d'un composé avec son réciproque !

• la loi est dite symétrisable à gauche ou inversible à gauche si tous les éléments de E sont inversibles à gauche;

• la loi est dite symétrisable à droite ou inversible à droite si tous les éléments de E sont inversibles à droite;

• la loi est dite symétrisable ou inversible si tous les éléments de E sont inversibles.

Si la loi est de plus associative, il y a unicité, pour les éléments symétrisables à gauche (respectivement à droite), de leur symétrique à gauche (resp. à droite). Et si un élément s est symétrisable à droite et à gauche alors ses symétriques à gauche et à droite sont forcément égaux entre eux et cet élément est donc symétrisable. Son symétrique est alors noté habituellement « s ^-1  ».

Exemples :

• 2 n'est pas symétrisable pour l'addition dans les entiers naturels;
• 2 est symétrisable, de symétrique -2, pour l’addition dans les entiers relatifs;
• 2 n’est pas inversible pour le produit dans les entiers relatifs;
• 2 est inversible, d’inverse , pour le produit dans les rationnels.

Remarque :

Lorsque la loi est notée additivement, le symétrique est plutôt appelé opposé, et quand la loi est notée multiplicativement le symétrique est plutôt appelé inverse.