Soustraction - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
La soustraction est l'une des opérations basiques de l'arithmétique. La soustraction combine deux ou plusieurs grandeurs du même type, appelées opérandes, pour donner un seul nombre, appelé la différence.
- Soustraire signifie diminuer en comptant.
- Soustraire b de a (calculer a − b) c'est trouver le nombre qui complèterait b pour donner a, c'est-à-dire le nombre d tel que b + d = a
Le signe de soustraction est le symbole « − ». Par exemple : on lit 3 − 2 = 1 comme « trois moins deux font un ».
Définition générale
Soit (G, +) un groupe additif. On définit une nouvelle loi de composition interne dans G, appelée « soustraction » et notée « − » par :
La soustraction est anticommutative.
Cas particulier des nombres
Ici nous travaillons dans (
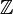
Formellement, la soustraction est une loi de composition interne sur un ensemble, notée - à condition toutefois que la soustraction soit toujours définie ( ce qui n'est, par exemple, pas le cas dans l'ensemble des entiers naturels

- elle n'est pas commutative. En effet a − b et b − a sont en général différents
- elle n'est pas associative. En effet (a − b) − c et a − (b − c) sont en général différents
- elle ne possède pas d'élément neutre. En effet, le seul élément neutre possible serait 0 et on a bien
- a − 0 = a, mais en général
- 0 − a est différent de a.
C'est la raison pour laquelle on préfère considérer une soustraction comme l'ajout (somme) de l'opposé à condition évidemment que cet opposé existe ( ce n'est pas toujours le cas dans

- L'opposé de a est le nombre noté (−a) qui, ajouté à a, donne 0 : a + (−a) = 0
- a − b peut alors s'écrire a + (−b)
Lorsqu’elle est appliquée sur une série comme en algorithmique c’est un décrément.