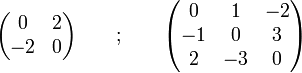Matrice antisymétrique - Définition
Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
La liste des auteurs de cet article est disponible ici.
Exemples
Les matrices suivantes sont antisymétriques :
Le cas où la matrice est à coefficients dans un anneau de caractéristique 2 est très particulier. Dans ce cas, -A=A donc A est antisymétrique si elle est symétrique. Dans tout ce qui suit, les coefficients de la matrices sont à coefficients dans un corps K de caractéristique différente de 2 (typiquement : le corps des réels).