Samedi 3 Mai 2025
Rechercher 🔍

Matrice d'inertie - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
- Introduction - Notation - Simplification et transport - Calcul des coefficients de la matrice

Calcul des coefficients de la matrice

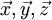
A,B et C sont des moments d'inertie par rapport à un axe (respectivement \vec x, \vec y, \vec z ).

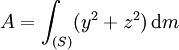
A = \int _{(S)} (y^2 + z^2) \,\mathrm dm
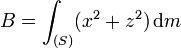
B = \int _{(S)} (x^2 + z^2) \,\mathrm dm
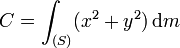
C = \int _{(S)} (x^2 + y^2) \,\mathrm dm

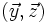
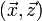
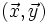
E,D et F sont des produits d'inertie, ils modélisent une asymétrie géométrique ou massique (solide non homogène) par rapport aux plans (\vec y, \vec z ) , ( \vec x, \vec z ) , ( \vec x, \vec y ) .

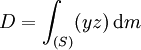
D = \int _{(S)} (yz) \,\mathrm dm
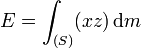
E = \int _{(S)} (xz) \,\mathrm dm
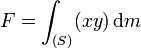
F = \int _{(S)} (xy) \,\mathrm dm

Remarque : En mécanique, l'unité la plus fréquemment utilisée est le kg.m²

Simplification et transport
- Introduction - Notation - Simplification et transport - Calcul des coefficients de la matrice
miniature
La face cachée de la Lune révèle une étrangeté 🌓
miniature
Piéger le CO2 sous terre indéfiniment, c'est possible ! 🌍
miniature
La plus lointaine cousine de la Voie Lactée jamais observée 🌀
miniature
Ce codex médiéval cache un secret dans son bois 🔍
miniature
Une éruption volcanique en 2018 responsable d'une explosion de vie 🌋
miniature
Un système d'exploitation pour les ordinateurs quantiques voit le jour 🖥️
miniature
Des singularités temporelles dans l'Univers ? 🕰️
miniature
Des fossiles de dinosaures mieux datés 🦖
miniature
Une gigantesque muraille de 10 milliards d'années-lumière dans l'Univers 🔭
miniature
Benchmark: les processeurs quantiques sous la loupe, quels sont les meilleurs ? 🏆
miniature
Découverte d'une "fourmi de l'enfer" vieille de 113 millions d'années 🐜
miniature
Le rôle méconnu de la décharge dans l'usure des batteries 🔋
miniature
1
La fonte des glaces déplace les pôles: quelles conséquences ? 🌍
miniature
L'appareil photo de votre smartphone peut détecter l'antimatière 📱
miniature
Cette étoile-zombie peut déformer les atomes à distance, et elle fonce dans notre galaxie ⭐
miniature
Un mosasaure géant découvert dans le Mississippi 🦕
miniature
Problème, les galaxies meurent plus tôt que prévu 🌀
miniature
Ce lien entre cannabis et troubles psychotiques 🧠
miniature
Une révolution dans le refroidissement des puces électroniques ? 🔥
miniature
Des parasites sous-marins filmés en train de vampiriser un poisson des abysses 👀
miniature
Lucy survole un astéroïde en forme de cacahuète 🚀
miniature
Découverte du fossile d'un dinosaure géant méconnu 🦕
miniature
Mars avait-elle un champ magnétique unilatéral ? 🔍
miniature
Des chimpanzés surpris à sociabiliser avec de l'alcool 🍇
miniature
Découverte macabre: ce gladiateur a été tué par un lion il y a 1 800 ans... en Grande-Bretagne 🦁
miniature
L'électroluminescence du graphène, une découverte inattendue ! 💡
miniature
Cet objet métallique n'a pas été fabriqué sur Terre 🔧
miniature
1
Cette innovation permet aux voitures électriques de charger 6 fois plus vite par grand froid ⚡
miniature
Cette super-Terre brûle les attentes des astronomes 🔥
miniature
Découverte exceptionnelle de fossiles d'amphibiens géants 🐸
miniature
Voici ce qui a causé les toutes premières inégalités de richesse 💰
miniature
Quelle est cette zone étrange dans l'Atlantique Nord ? 🌊
miniature
Cette planète orbite à angle droit autour de deux étoiles, une première ! 🔭
miniature
Des cellules solaires flexibles battent des records d'efficacité ⚡
miniature
Ce dispositif reproduit les trous noirs et trous blancs en laboratoire 🌀
miniature
Record établi pour un transistor en diamant 💎
miniature
Les sursauts radio rapides trahissent enfin leur origine cosmique 📡
miniature
Ces biomarqueurs sanguins prédisent la démence 10 ans à l'avance 🧠
miniature
Découverte majeure: des médicaments 23 fois plus efficaces contre le cancer 💊
miniature
Les oscillations collectives des foules humaines denses 🔁
miniature
Une forme inconnue de la matière détectée au LHC ? ⚛️
miniature
Le sel, un facteur méconnu de l'obésité ? 🧂
miniature
L'Univers en rotation, une réponse élégante à ce problème astrophysique majeur 🌀
miniature
Découverte tectonique majeure sous les Petites Antilles 🌍
miniature
1
Peut-on geler en chauffant ? ❄️
miniature
Une peau électronique pour doter les robots du sens du toucher 👌
miniature
Invention d'un bois semi-transparent avec une technique...surprenante ! 🌳
miniature
Le cancer inscrit dans nos gènes dès la naissance ? 🧬
miniature
Des supernovae à l'origine de deux extinctions massives sur Terre ? 💥
miniature
Le passé verdoyant du plus grand désert du monde 🐪
Page générée en 0.066 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise