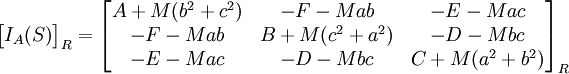Matrice d'inertie - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
La matrice d'inertie est un outil mathématique utilisé pour décrire les efforts d'inertie appliqués à un solide.
Notation
Cette matrice s'écrit :
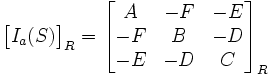
avec a point quelconque du solide (S), R repère orthonormé direct, A,B,C moments d'inertie par rapport à
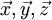
Simplification et transport
Pour simplifier l'écriture de la matrice d'inertie, on choisit de l'écrire en G, centre d'inertie du solide (S). De plus, on choisit un repère compatible avec les plans de symétrie de (S), s'ils existent.
Exemple d'un arbre de matériau homogène de longueur L, de rayon R, de masse M et avec pour axe principal
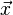
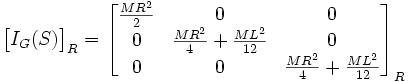
Nota : même si le solide ne présente pas de plans de symétrie, les propriétés mathématiques de la matrice d'inertie (matrice symétrique, somme des termes diagonaux strictement positive - sauf si le solide est réduit à un point !) sont telles qu'il existe toujours un repère (en fait six par permutation circulaire et changement de signes, en se limitant aux repères directs) dans lequel la matrice ne comporte que des termes diagonaux. Ce repère s'appelle "repère propre d'inertie" et les trois moments d'inertie correspondants "moments d'inertie principaux".
Pour écrire une matrice d'inertie en un autre point on applique le théorème de Huygens.
Exemple de transport de matrice d'inertie.
Soit
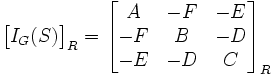
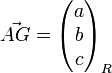
on aura