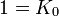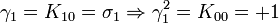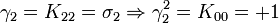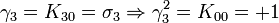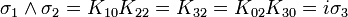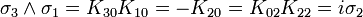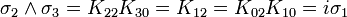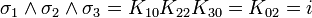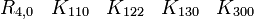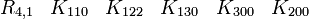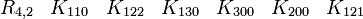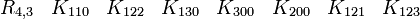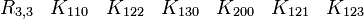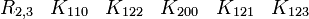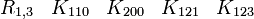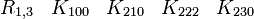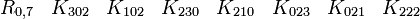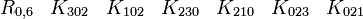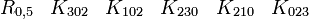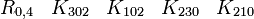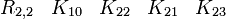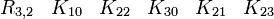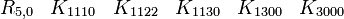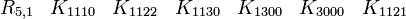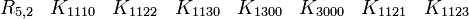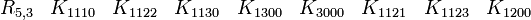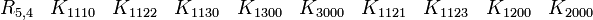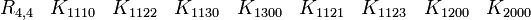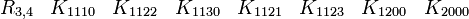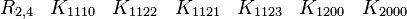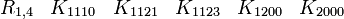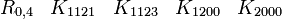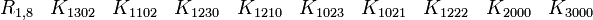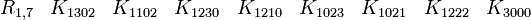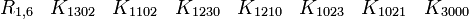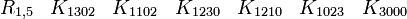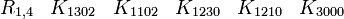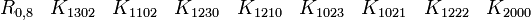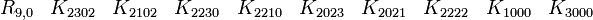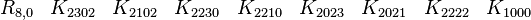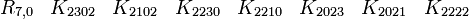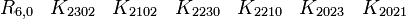Vendredi 1er Août 2025
Rechercher 🔍

Représentation des algèbres de Clifford - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
- Introduction - Représentations matricielles des algèbres de Clifford réelles - L'algèbre de Clifford réelle R2,0 - Intermezzo : le système K pour nommer les matrices - L'algèbre de Clifford R2,1 - L'algèbre de Clifford réelle R1,1 - L'algèbre de Clifford R0,3 - L'algèbre de Clifford R0,2 - L'algèbre de Clifford réelle R3,1 - L'algèbre de Clifford R3,0 - Représentations avec les matrices réelles 8x8 - Autres représentations avec les matrices réelles 4x4 - Représentations avec les matrices réelles 16x16

L'algèbre de Clifford R3,0

Ceci est la célèbre algèbre de Pauli, si vous pensez à K02 pour i et K00 pour 1. Nous avons trois Kplus pour base de vecteurs.

catégorie 0 (le scalaire)

\begin{matrix} 1 = K_0 \end{matrix}

catégorie 1 (les vecteurs)

\gamma_1 = K_{10} = \sigma_1 \Rightarrow \gamma_1^2 = K_{00} = +1
\gamma_2 = K_{22} = \sigma_2 \Rightarrow \gamma_2^2 = K_{00} = +1
\gamma_3 = K_{30} = \sigma_3 \Rightarrow \gamma_3^2 = K_{00} = +1

La signature est ( + + + )

catégorie 2 (les bivecteurs)

\sigma_1 \land \sigma_2 = K_{10} K_{22} = K_{32} = K_{02} K_{30}= i \sigma_3
\sigma_3 \land \sigma_1 = K_{30} K_{10} = -K_{20} = K_{02}K_{22} = i \sigma_2
\sigma_2 \land \sigma_3 = K_{22} K_{30} = K_{12} = K_{02} K_{10} = i \sigma_1

catégorie 3 (le pseudoscalaire)

\sigma_1 \land \sigma_2 \and \sigma_3 = K_{10} K_{22} K_{30} = K_{02} = i

Donc i est le pseudoscalaire et les équations pour les bivecteurs signifient en fait que chaque bivecteur est le dual de Hodge de l'un des vecteurs qui n'est pas une partie du bivecteur.

Représentations avec les matrices réelles 8x8

\begin{matrix} R_{4,0} &K_{110} &K_{122} &K_{130} &K_{300} \end{matrix}
\begin{matrix} R_{4,1} &K_{110} &K_{122} &K_{130} &K_{300} &K_{200} \end{matrix}
\begin{matrix} R_{4,2} &K_{110} &K_{122} &K_{130} &K_{300} &K_{200} &K_{121} \end{matrix}
\begin{matrix} R_{4,3} &K_{110} &K_{122} &K_{130} &K_{300} &K_{200} &K_{121} &K_{123} \end{matrix}
\begin{matrix} R_{3,3} &K_{110} &K_{122} &K_{130} &K_{200} &K_{121} &K_{123} \end{matrix}
\begin{matrix} R_{2,3} &K_{110} &K_{122} &K_{200} &K_{121} &K_{123} \end{matrix}
\begin{matrix} R_{1,3} &K_{110} &K_{200} &K_{121} &K_{123} \end{matrix}

Cette dernière est très importante en physique puisqu'elle est l'algèbre de Clifford la plus utilisée pour le travail dans l'espace-temps de Minkowski. La signature est ( + - - - ). Voir convention de signe. Les représentations les plus utilisées sont

\begin{matrix} R_{1,3} &K_{100} &K_{210} &K_{222} &K_{230} \end{matrix}

En s'intéressant aux matrices réelles 8 x 8, on peut former 7 matrices Kmoins anticommutatives. Ils forment un ensemble de bases pour l'algèbre de Clifford réelle non-universelle R0,7

\begin{matrix} R_{0,7} &K_{302} &K_{102} &K_{230} &K_{210} &K_{023} &K_{021} &K_{222} \end{matrix}
\begin{matrix} R_{0,6} &K_{302} &K_{102} &K_{230} &K_{210} &K_{023} &K_{021} \end{matrix}
\begin{matrix} R_{0,5} &K_{302} &K_{102} &K_{230} &K_{210} &K_{023} \end{matrix}
\begin{matrix} R_{0,4} &K_{302} &K_{102} &K_{230} &K_{210} \end{matrix}

(Pour R0,3, nous avons montré qu'une seule a besoin de matrices réelles 4x4)

Autres représentations avec les matrices réelles 4x4

\begin{matrix} R_{2,2} &K_{10} &K_{22} &K_{21} &K_{23} \end{matrix}
\begin{matrix} R_{3,2} &K_{10} &K_{22} &K_{30} &K_{21} &K_{23} \end{matrix}

Représentations avec les matrices réelles 16x16

\begin{matrix} R_{5,0} &K_{1110} &K_{1122} &K_{1130} &K_{1300} &K_{3000} \end{matrix}
\begin{matrix} R_{5,1} &K_{1110} &K_{1122} &K_{1130} &K_{1300} &K_{3000}&K_{1121} \end{matrix}
\begin{matrix} R_{5,2} &K_{1110} &K_{1122} &K_{1130} &K_{1300} &K_{3000}&K_{1121} &K_{1123} \end{matrix}
\begin{matrix} R_{5,3} &K_{1110} &K_{1122} &K_{1130} &K_{1300} &K_{3000}&K_{1121} &K_{1123} &K_{1200} \end{matrix}
\begin{matrix} R_{5,4} &K_{1110} &K_{1122} &K_{1130} &K_{1300} &K_{3000}&K_{1121} &K_{1123} &K_{1200} &K_{2000} \end{matrix}
\begin{matrix} R_{4,4} &K_{1110} &K_{1122} &K_{1130} &K_{1300} &K_{1121} &K_{1123} &K_{1200} &K_{2000} \end{matrix}
\begin{matrix} R_{3,4} &K_{1110} &K_{1122} &K_{1130} &K_{1121} &K_{1123} &K_{1200} &K_{2000} \end{matrix}
\begin{matrix} R_{2,4} &K_{1110} &K_{1122} &K_{1121} &K_{1123} &K_{1200} &K_{2000} \end{matrix}
\begin{matrix} R_{1,4} &K_{1110} &K_{1121} &K_{1123} &K_{1200} &K_{2000} \end{matrix}
\begin{matrix} R_{0,4} &K_{1121} &K_{1123} &K_{1200} &K_{2000} \end{matrix}
\begin{matrix} R_{1,8} &K_{1302} &K_{1102} &K_{1230} &K_{1210} &K_{1023} &K_{1021} &K_{1222} &K_{2000} &K_{3000} \end{matrix}
\begin{matrix} R_{1,7} &K_{1302} &K_{1102} &K_{1230} &K_{1210} &K_{1023} &K_{1021} &K_{1222} &K_{3000} \end{matrix}
\begin{matrix} R_{1,6} &K_{1302} &K_{1102} &K_{1230} &K_{1210} &K_{1023} &K_{1021} &K_{3000} \end{matrix}
\begin{matrix} R_{1,5} &K_{1302} &K_{1102} &K_{1230} &K_{1210} &K_{1023} &K_{3000} \end{matrix}
\begin{matrix} R_{1,4} &K_{1302} &K_{1102} &K_{1230} &K_{1210} &K_{3000} \end{matrix}

R1,3 a besoin seulement de matrices réelle 4x4

\begin{matrix} R_{0,8} &K_{1302} &K_{1102} &K_{1230} &K_{1210} &K_{1023} &K_{1021} &K_{1222} &K_{2000} \end{matrix}

R0,7 a besoin seulement de matrices réelles 8x8

\begin{matrix} R_{9,0} &K_{2302} &K_{2102} &K_{2230} &K_{2210} &K_{2023} &K_{2021} &K_{2222} &K_{1000} &K_{3000} \end{matrix}
\begin{matrix} R_{8,0} &K_{2302} &K_{2102} &K_{2230} &K_{2210} &K_{2023} &K_{2021} &K_{2222} &K_{1000} \end{matrix}
\begin{matrix} R_{7,0} &K_{2302} &K_{2102} &K_{2230} &K_{2210} &K_{2023} &K_{2021} &K_{2222} \end{matrix}
\begin{matrix} R_{6,0} &K_{2302} &K_{2102} &K_{2230} &K_{2210} &K_{2023} &K_{2021} \end{matrix}

R5,0 a besoin seulement de matrices réelles 8x8

L'algèbre de Clifford réelle R3,1
- Introduction - Représentations matricielles des algèbres de Clifford réelles - L'algèbre de Clifford réelle R2,0 - Intermezzo : le système K pour nommer les matrices - L'algèbre de Clifford R2,1 - L'algèbre de Clifford réelle R1,1 - L'algèbre de Clifford R0,3 - L'algèbre de Clifford R0,2 - L'algèbre de Clifford réelle R3,1 - L'algèbre de Clifford R3,0 - Représentations avec les matrices réelles 8x8 - Autres représentations avec les matrices réelles 4x4 - Représentations avec les matrices réelles 16x16
miniature
🔭 Cette observation suggère que tout pourrait venir de la ceinture d'astéroïdes
miniature
🦴 Comment les pythons digèrent-ils les os sans laisser de trace ?
miniature
💫 Comment un pulsar milliseconde a trompé les astronomes pendant des années ?
miniature
🌱 Par évolution dirigée, le MIT a fortement amélioré l'efficacité de la photosynthèse
miniature
🌍 Une météorite a-t-elle modifié le Grand Canyon il y a 56 000 ans ?
miniature
🕒 Le lien surprenant entre repas tardifs, santé et prise de poids
miniature
💥 Cette collision de trous noirs est si massive qu'elle fait trembler nos lois de l'astrophysique
miniature
1
🩺 Cancer: des cellules "oubliées" passent à l'offensive
miniature
🔭 Quel est cet objet mystérieux, lié à Neptune dans une orbite jamais vue auparavant ?
miniature
🍄 Découverte surprenante: vivre 25 ans de plus grâce aux "champignons magiques" ?
miniature
🩺 L'âge des premières règles est un indicateur de la santé à venir
miniature
⚛️ Cette découverte pourrait expliquer pourquoi notre Univers existe
miniature
🌋 Découverte majeure sous Yellowstone grâce à l'IA
miniature
1
🏹 Violence préhistorique: découverte d'un surprenant homicide raté
miniature
🌌 Des scientifiques découvrent dans l'Univers un gigantesque filament de matière "manquante"
miniature
🐱 Ce chat a aidé à découvrir un virus inconnu... deux fois !
miniature
🪐 Cette planète provoque la fureur de son étoile
miniature
👂 Et si nous pouvions entendre une caresse ?
miniature
👑 Cette découverte archéologique révèle les prémices des pharaons
miniature
🦈 Le requin bleu peut changer de couleur, comme un caméléon
miniature
🌞 La NASA dévoile les images les plus proches jamais prises du soleil
miniature
⏳ Il est maintenant possible de mesurer le vieillissement avec précision
miniature
🚀 1 pétabit/seconde: ce nouveau record permet de télécharger tout le catalogue de Netflix en 1 seconde
miniature
🩺 Donald Trump et insuffisance veineuse chronique: une maladie aux complications graves
miniature
🌍 Les barrages construits par l'Homme ont déplacé les pôles de la Terre
miniature
🍖 Les Néandertaliens avaient leurs propres recettes de cuisine, qui veut goûter ?
miniature
🔭 À l'observatoire Rubin, le grand film de l'Univers démarre
miniature
🧬 Réparer l'ADN cassé et sauver nos cellules
miniature
🪨 Découverte d'un important gisement de "kryptonite" en Europe, au potentiel énergétique hors norme
miniature
🕰️ La Terre possède sa propre horloge géologique
miniature
☄️ Les scientifiques ne comprennent pas la trajectoire des fragments de l'astéroïde Dimorphos
miniature
🦖 Les protéines survivent bien plus longtemps que l'ADN, et pourraient réécrire l'histoire
miniature
📢 Pourquoi certains sons nous réveillent, et d'autres non ?
miniature
🌋 Des BLOBS se déplacent sous nos pieds: des structures à l'origine d'éruptions cataclysmiques
miniature
🌀 Une centaine de galaxies invisibles autour de la Voie lactée ?
miniature
🐛 Ces chenilles "plastivores" transforment le plastique en graisse corporelle
miniature
⛈️ La météo sur Titan vue par James Webb et Keck
miniature
💀 Cette pieuvre tue avec un venin 1200 fois plus toxique que le cyanure, et il n'y a pas d'antidote
miniature
👀 Une "Bête" géante observée en train de danser au-dessus du Soleil
miniature
⏳ Des séismes lents filmés pour la première fois en temps réel. De quoi s'agit-il ?
miniature
✨ Découverte "d'étoiles ratées" de l'extrême: que nous apprennent-elles ?
miniature
🎨 Pourquoi les hommes sont-ils beaucoup plus souvent daltoniens que les femmes ?
miniature
☄️ Un visiteur interstellaire bientôt visible à l'œil nu dans le ciel ?
miniature
🧬 Vous avez des migraines ? Vous avez peut-être du crâne de Néandertal en vous !
miniature
🩺 L'IMC doit être remplacé: voici pourquoi et par quoi
miniature
👽 Découverte de conditions propices à la vie sur Titan, la lune de Saturne
miniature
🦖 Insolite: Ce musée trouve un fossile de dinosaure... sous son parking !
miniature
🍦 Pourquoi les glaces nous donnent parfois mal à la tête ?
miniature
🤔 Personne ne comprend ces mystérieux dodecaèdres romains
miniature
🌋 Vidéo - Un volcan de boue entre en éruption devant un temple à Taiwan
Page générée en 0.754 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise