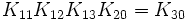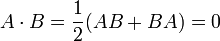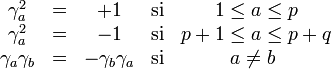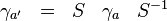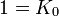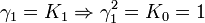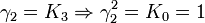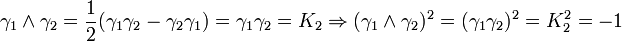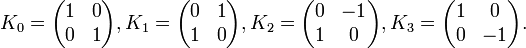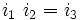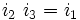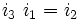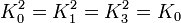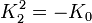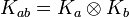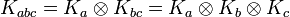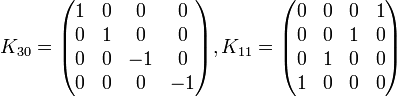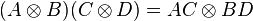Représentation des algèbres de Clifford - Définition

Introduction

En mathématiques, les représentations des algèbres de Clifford sont aussi connues sous le nom modules de Clifford. En général, une algèbre de Clifford C est une algèbre centrale simple sur une certaine extension de corps L d'un corps K sur lequel la forme quadratique Q définissant C est définie.

La théorie algébrique des modules de Clifford a été mise au point par M. F. Atiyah, R. Bott et A. Shapiro dans l'article Clifford Modules (Topology 3 (Suppl. 1) (1964), 3–38).

Représentations matricielles des algèbres de Clifford réelles

Nous aurons besoin d'étudier les matrices anticommutatives (AB = -BA) les vecteurs orthogonaux anticommutent dans les algèbres de Clifford.

Pour l'algèbre de Clifford réelle , nous avons besoin de p + q matrices mutuellement anticommutatives, dont p ont pour carré +1 et q ont pour carré - 1.

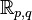
Une telle base de matrices gamma n'est pas unique. On peut toujours obtenir un autre ensemble de matrices gamma satisfaisant la même algèbre de Clifford par une transformation de similarité.

où S est une matrice non-singulière. Les ensembles et appartiennent à la même classe d'équivalence.

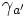
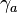
L'algèbre de Clifford réelle R2,0

p = 2 et q = 0, donc nous avons besoin de 2 Kplus comme base de vecteurs

catégorie 0 (le scalaire)

catégorie 1 (les vecteurs)

catégorie 2 (le pseudoscalaire)

n = p + q = 2 et nous avons 2² = 4 éléments donc, c'est ce que I. Porteous appelle une algèbre de Clifford universelle.

Intermezzo : le système K pour nommer les matrices

Nous présentons d'abord une méthode élégante pour nommer les matrices

À noter que K₀ est la matrice identité. Les noms ont été choisis de manière qu'il existe une règle simple pour se souvenir des produits :

.

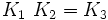
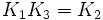
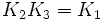
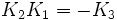
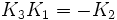
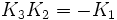
Incrémenter l'index donne un résultat positif. Décrémenter l'index donne un résultat négatif.

Attention ! Il n'existe PAS les mêmes relations valides pour la base standard des quaternions. Si vous vouliez nommer vous obtiendriez

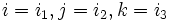
donc, la dernière règle est différente. Nous verrons plus tard que les quaternions purs i,j et k peuvent être représentés par K₁₂,K₂₀ et K₃₂

Remarquez que

K₂ est la seule avec un carré négatif, donc elle peut être regardée comme la représentation la plus simple de i

Nous donnons un nom à tous les produits de Kronecker possibles (voir produit matriciel) :

Quelques exemples

Chaque index possède son niveau ( 2x2, 4x4, 8x8, 16x16, ...)

K₁₃ est une K₃ de niveau 2x2 et une K₁ de niveau 4x4. Avec cette notation, il est très simple de multiplier de grandes matrices puisque

Regardons un exemple

K₁₂₃ K₂₂₂ = K₃₀₁

niveau 8x8 1 fois 2 donne 3

niveau 4x4 2 fois 2 donne 0 mais souvenez-vous du signe moins

niveau 2x2 3 fois 2 donne 1 mais souvenez-vous du signe moins

(les deux signes moins s'annule donc le résultat est K₃₀₁ )

Nous pouvons maintenant démarrer la construction d'ensembles de matrices orthogonales mutuellement anticommutatives (voir matrice orthogonale), quelquefois appelées matrices de Dirac. Il est évident que deux de telles matrices anticommutent si elles anticommutent dans un nombre impair d'index (l'index o commute avec tous les autres indices).

K₁₃ par exemple anticommute avec

K₀₁,K₀₂,K₁₁,K₁₂,K₂₀,K₂₃,K₃₀,K₃₃

et commute avec

K₀₀,K₁₀,K₁₃,K₂₁,K₂₂,K₃₁,K₃₂.

Si l'index 2 apparaît un nombre pair de fois dans le nom alors le carré de la matrice est plus la matrice identité, appelons-la une Kplus

en voici des exemples : K₁, K₂₂, K₃₁₁, K₂₂₂₂

Si l'index 2 apparaît un nombre impair de fois dans le nom alors le carré de la matrice est moins la matrice identité, appelons-la une Kmoins

en voici des exemples : K₂, K₂₂₂, K₂₁₁, K₁₂₂₂

Nous avons maintenant une manière très simple de construction d'ensembles très larges de matrices anticommutatives.

Démarrons avec un ensemble existant

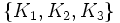
Insérons un nouvel index constant (par exemple un 1 dans la premère position) et vous obtenez

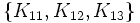
Puis ajoutons deux matrices supplémentaires qui anticommutent dans le nouveau niveau et commutons dans l'ancien niveau (au moyen du zéro à l'index 0)

Donc, nous obtenons

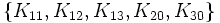
Autres exemples

{K₂₁, K₂₂, K₂₃, K₁₀, K₃₀}

{K₃₁, K₃₂, K₃₃, K₁₀, K₂₀}

{K₁₁₁, K₁₁₂, K₁₁₃, K₁₂₀, K₁₃₀, K₂₀₀, K₃₀₀}

{K₂₁₁, K₂₁₂, K₂₁₃, K₂₂₀, K₂₃₀, K₁₀₀, K₃₀₀}

{K₃₁₁, K₃₁₂, K₃₁₃, K₃₂₀, K₃₃₀, K₁₀₀, K₂₀₀}

Nous obtenons toujours un ensemble avec un nombre impair de matrices et il existe toujours une Kplus de plus qu'une Kmoins.

Chacune d'elles peut être écrite comme le produit de toutes les autres. Exemple :