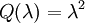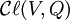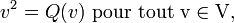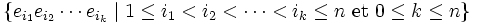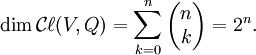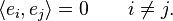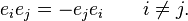Algèbre de Clifford - Définition

Introduction

En mathématiques, les algèbres de Clifford sont des algèbres associatives importantes au sein des théories des formes quadratiques, des groupes orthogonaux et en physique. Elles peuvent être vues comme l'une des généralisations possibles des nombres complexes et des quaternions. Elles ont été nommées en l'honneur du mathématicien anglais William Kingdon Clifford.

Une certaine familiarité avec les bases de l'algèbre multilinéaire sera très utile à la lecture de cet article.

Introduction et propriétés de base

Précisément, une algèbre de Clifford est une algèbre associative unitaire qui est engendrée par un espace vectoriel V muni d'une forme quadratique Q.

L'algèbre de Clifford est l'algèbre « la plus générale » engendrée par V soumise à la condition

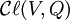
où le produit v² est pris à l'intérieur de l'algèbre et le réel Q(v) est identifié à Q(v)·1, 1 désignant l'unité de l'algèbre. Si la caractéristique du corps de base K n'est pas 2, alors on peut ré-écrire cette identité fondamentale sous la forme

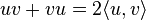
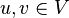
pour tout

où est la forme bilinéaire symétrique associée à Q.

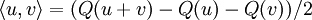
Cette idée d'algèbre « la plus générale » soumise à cette identité peut être formellement exprimée à travers la notion de propriété universelle (voir ci-dessous).

Les algèbres de Clifford sont directement reliées aux algèbres extérieures. En fait, si Q = 0 alors l'algèbre de Clifford est simplement l'algèbre extérieure . Pour Q différent de zéro, il existe un isomorphisme canonique linéaire entre et toutes les fois que le corps de base K n'est pas de caractéristique 2. C’est-à-dire qu'ils sont naturellement isomorphes comme espaces vectoriels mais avec des multiplications différentes. La multiplication de Clifford est plus riche que le produit extérieur puisqu'il fait usage d'une information supplémentaire fournie par Q.

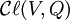
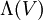
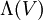
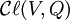
Les formes quadratiques et les algèbres de Clifford de caractéristique 2 forment un cas exceptionnel. En particulier, si la caractéristique de K = 2, il n'est pas vrai qu'une forme quadratique est déterminée par sa forme bilinéaire symétrique, ou que chaque forme quadratique admet une base orthogonale. Beaucoup de résultats dans cet article incluent la condition que la caractéristique n'est pas 2, et sont faux si cette condition est enlevée.

Base et dimension

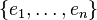
Si la dimension de V est n et est une base de V, alors l'ensemble

est une base de . Le produit vide (k = 0) est défini comme l'élément neutre multiplicatif. Pour chaque valeur de k, il existe éléments de la base, donc, la dimension totale de l'algèbre de Clifford est

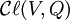
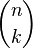
Si la caractéristique n'est pas 2, il existe un ensemble de bases privilégiées pour V : les bases orthogonales. Une base orthogonale est telle que

où <·,·> est la forme bilinéaire symétrique associée à Q. L'identité de Clifford fondamentale implique que pour une base orthogonale

Ceci rend la manipulation des vecteurs de la base orthogonale tout à fait simple. Etant donné un produit de vecteurs distincts de la base orthogonale, on peut les placer dans un ordre standard en incluant un signe correspondant au nombre de permutations nécessaires pour les ordonner correctement (i.e. la signature de la permutation ordonnée).

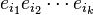
On peut aisément étendre la forme quadratique sur V vers une forme quadratique sur en demandant que les éléments distincts soient orthogonaux entre eux, et en posant :

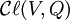
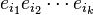
En particulier Q(1) = 1 et la forme quadratique sur un scalaire est simplement . Ainsi, les bases orthogonales de V peuvent être étendues en une base orthogonale de . La forme quadratique définie de cette manière est en fait indépendante de la base orthogonale choisie (une formulation indépendante de la base sera donnée plus bas).