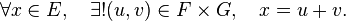Sous-espace supplémentaire - Définition

Définition

Dans toute la suite de l'article, F et G sont deux sous-espaces vectoriels d'un même espace E.

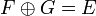
Propriétés

Le critère 6 fournit un procédé simple pour construire deux sous-espaces supplémentaires : couper une base de E en deux parties complémentaires et prendre les sous-espaces engendrés par ces deux parties. En terme de base, on réduit ainsi la notion de supplémentaire à celle de complémentaire. Si on part d'une base de F et qu'on utilise le théorème de la base incomplète pour construire une base de E, les vecteurs qu'on a, ce faisant, ajoutés à la base de F engendrent un supplémentaire de F. Ainsi,

Tout sous-espace F de E possède des supplémentaires.

Le critère 4 permet de montrer que tout supplémentaire G de F est isomorphe à l'espace vectoriel quotient E / F. Ainsi,

tous les supplémentaires de F sont isomorphes.

Ils ont donc la même dimension, finie ou infinie. Cette dimension commune est appelée codimension de F.