Sous-espace supplémentaire - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, plus précisément en algèbre linéaire, deux sous-espaces vectoriels d'un même espace vectoriel sont supplémentaires dans cet espace si tout vecteur de l'espace se décompose de façon unique en une somme d'un vecteur de chacun des deux sous-espaces. L'existence pour tout vecteur d'une telle décomposition revient à dire que la somme des deux sous-espaces est égale à l'espace tout entier, et l'unicité équivaut à ce que cette somme soit directe (ce qui se caractérise par le fait que l'intersection des deux sous-espaces est réduite au vecteur nul).
Confusion fréquente
La notion de supplémentaire est souvent confondue avec la notion ensembliste de complémentaire qui est très différente. Les différences entre les deux notions sont nombreuses. Tout d'abord, il y a unicité du complémentaire, alors que pour un sous-espace donné, il existe généralement une infinité de supplémentaires différents. Ensuite l'intersection d'un sous-espace avec un supplémentaire n'est pas vide mais contient le vecteur nul (et uniquement celui-là). Enfin, la réunion d'un sous-espace et d'un supplémentaire n'est pas égale à tout l'espace, plus subtilement, elle engendre cet espace. De façon intuitive, deux sous-espaces supplémentaires contiennent exactement l'information dont on a besoin pour reconstituer l'espace entier.
Critères
Théorème — Les propriétés suivantes sont équivalentes :
- F et G sont supplémentaires,
- l'application somme
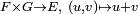
- E = F + G et F ∩ G = { 0 },
- il existe un projecteur q de E (c'est-à-dire un endomorphisme de E vérifiant q o q = q) de noyau F et d'image G,
- il existe deux projecteurs p et q de E dont la somme vaut l'identité et dont les images respectives sont F et G,
- il existe une base de F et une base de G dont la juxtaposition forme une base de E.
Montrons que 1, 2, 3 sont équivalents, que
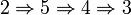
-

-
-
-
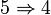
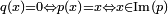
-
-
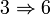
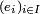
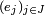
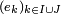
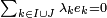
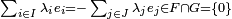
-
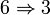
En dimension finie, on en déduit d'autres critères, dont le plus utile est le suivant :
Si E est de dimension finie alors F et G sont supplémentaires si et seulement si F ∩ G = { 0 } et dim(F) + dim(G) = dim(E).

















































