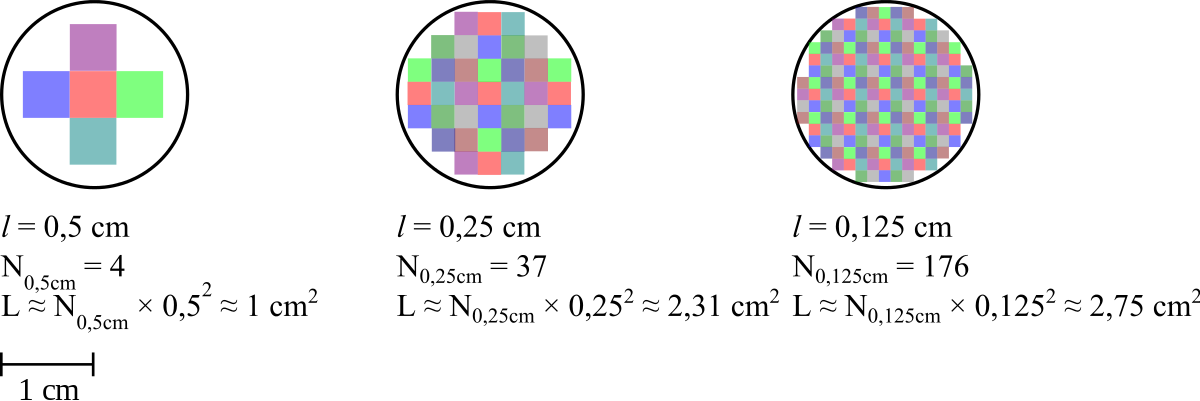Dimension - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Dans le sens commun, la notion de dimension renvoie à la taille ; les dimensions d'une pièce sont sa longueur, sa largeur et sa profondeur/son épaisseur, ou bien son diamètre si c'est une pièce de révolution.
En physique et en mathématique, la notion de dimension signifie d'abord le nombre de directions indépendantes, puis a été étendu.
Technique
Dans le domaine de la mécanique, le terme « dimension » renvoie à la taille d'une pièce.
Dans l'absolu, les dimensions d'une pièce peuvent être choisies de manière totalement arbitraire, l'important étant qu'elles soient compatibles avec l'utilisation finale de la pièce. Dans un but de normalisation, il est toutefois préférable d'utiliser comme dimensions linéaires nominales des valeurs de la « série de Renard ».
Dans la pratique de tous les jours, le terme renvoie à la taille d'un objet. Nous avons par exemple
- objet de 350 × 250 × 255 mm.
- description : (L)ongueur × (l)argeur × (h)auteur.
- forme : D = (L × l × h)
Mathématiques
Dimension d'un espace vectoriel
En algèbre linéaire, la dimension d'un espace vectoriel E sur un corps K est le cardinal commun à toutes les bases de E. Une base est une famille libre maximale ou une famille génératrice minimale. Si ce cardinal est fini, il représente le nombre de vecteurs de base à introduire pour écrire les coordonnées d'un vecteur. Cette notion conduit à la classification des espaces vectoriels : deux espaces vectoriels sur K sont isomorphes si ils ont même dimension.
Par exemple, l'espace vectoriel réel des suites réelles est de dimension infinie. Dans un tel espace, il existe des familles libres finies arbitrairement grandes, mais aucune famille génératrice finie.
Dimension d'une variété topologique ou d'une variété différentiable
La dimension d'une variété topologique est une généralisation courbée de la notion de dimension d'un espace vectoriel. Comme une variété topologique est définie par recollement de morceaux homéomorphes à des ouverts des espaces vectoriels

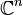
Dimension fractale
Approche didactique
Mais la définition de la « dimension » donnée ci-dessus est insuffisante, notamment dans le cas des fractales.
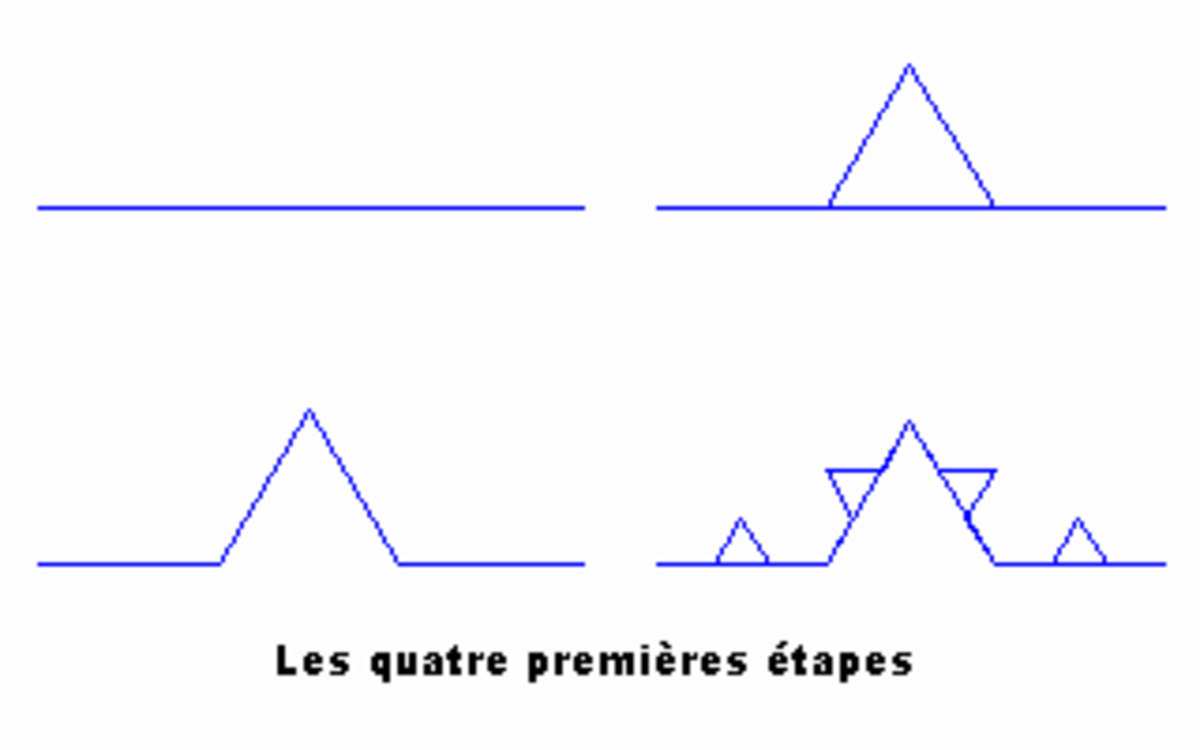
De manière simplifiée et en première approximation (voir Fractale pour une meilleure définition), un objet fractal est un objet ayant une homothétie interne, c'est-à-dire qu'une portion de l'objet est identique à l'objet complet. Considérons un exemple simple, le flocon de Koch : cette courbe est construite de manière récursive, on part d'un segment de droite, et on remplace chaque segment par un segment avec un chevron au milieu.
On répète cette opération à l'infini. Cette courbe est une ligne (donc de dimension 1, au sens ordinaire). Sa longueur est infinie, puisqu'à chaque étape on multiplie sa longueur par 4/3, et qu'il y a un nombre infini d'étapes. Pourtant, et contrairement à une droite infinie, on peut toujours trouver une courbe de longueur finie aussi proche que l'on veut de la courbe de von Koch. On peut donc dire en fait que si on trouve que la longueur de la courbe de von Koch est infinie, c'est qu'on l'évalue dans une « mauvaise » dimension, et qu'en mesurant « mieux », on aurait une mesure « utile », finie.
Nous avons besoin de revenir sur la notion d'étalon en physique :
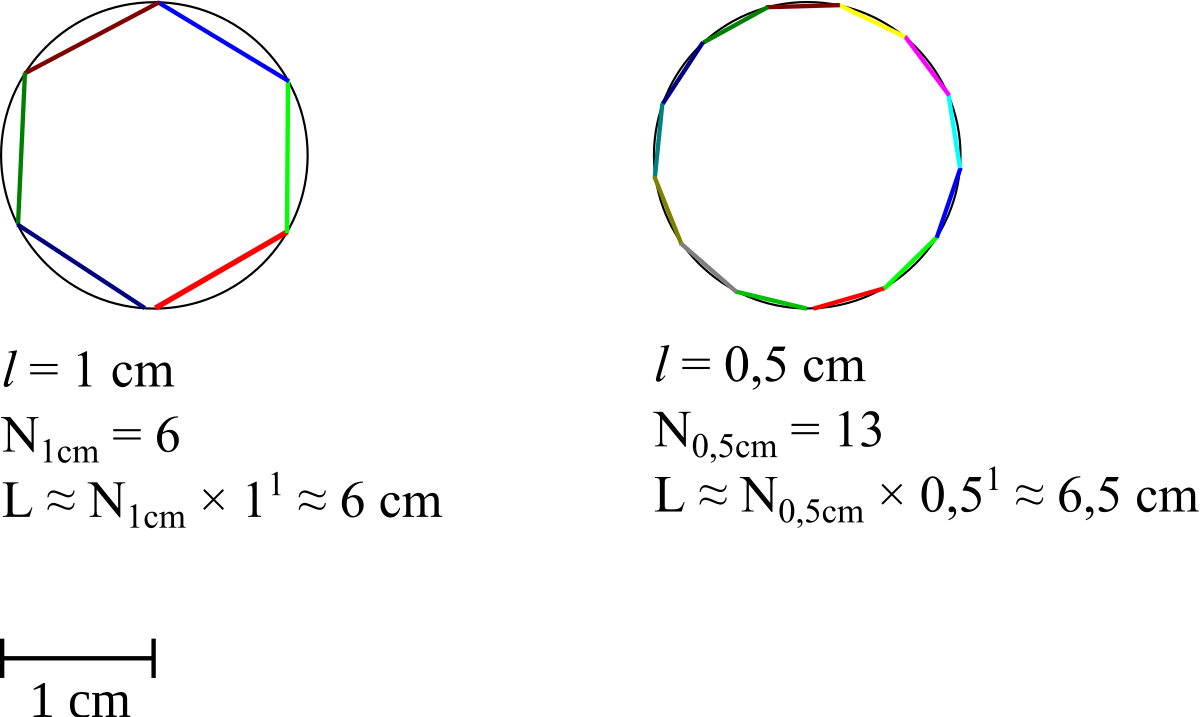
- L'étalon de longueur est une règle de longueur fixe (dimension 1) : pour mesurer une longueur, on regarde combien de règles tiennent bout-à-bout sur la courbe ;
- L'étalon de surface est un carreau (carré) de côté fixe (dimension 2) : pour mesurer la surface, on regarde combien de carreaux on peut poser côte-à-côte sur la surface ;
- L'étalon de volume est un pavé (cube) d'arête fixe (dimension 3) : pour mesurer le volume, on regarde combien de pavés on peut empiler dans l'objet.
On ne peut évaluer la longueur que d'un objet de dimension 1 : même en prenant une règle minuscule, un point ne pourra jamais la contenir, et à l'inverse sur une surface, on peut mettre un nombre infini de règles côte-à-côte (celles-ci ont une épaisseur nulle).
De même, on ne peut évaluer l'aire que d'un objet de dimension 2 : un point ou une courbe ne pourra jamais être pavé par des carreaux (même très petits), et dans un volume, on peut empiler un nombre infini de carreaux (ceux-ci ont une épaisseur nulle).
On ne peut évaluer le volume que d'un objet à trois dimensions, puisqu'on ne peut pas mettre de pavé dans un point, une courbe ni une surface.
Ainsi, si l'on appelle do la dimension de l'objet et de celle de l'étalon, on a :
- si de > do, la mesure donne 0 : on ne peut pas mettre un seul étalon dans l'objet ; c'est le cas pour la courbe de von Koch lorsqu'on utilise une mesure avec une aire, ce qui indique donc que sa dimension fractale est strictement inférieure à 2.
- si de < do, la mesure donne ∞ : on peut mettre autant d'étalons qu'on veut dans l'objet ; c'est le cas pour la courbe de von Koch lorsqu'on utilise une mesure avec une longueur, ce qui indique donc que sa dimension fractale est strictement supérieure à 1.
- si de = do, la mesure peut donner (si l'objet mesuré n'est pas infini) un nombre fini, le nombre d'étalons qu'il faut pour couvrir l'objet ; notre problème est donc de trouver (si elle existe) la « bonne » dimension, celle qui nous donnera une mesure finie (si l'objet est fini).
Pour faire cette mesure, la « taille » de l'étalon n'est pas sans effet. Si l'étalon est trop grand, il ne rentre pas dans l'objet (la mesure est nulle), mais en prenant des étalons de plus en plus petits, on obtient (d'habitude) des mesures qui se rapprochent. Si, pour mesurer une ligne, on utilise une règle de longueur ℓ, plus ℓ est petit, plus on pourra mettre d'étalons dans l'objet à mesurer. La mesure est le produit du nombre d'étalons par la taille de l'étalon : Si l'on fait tenir Nℓ règles de longueur ℓ, la mesure sera
- M(ℓ) = Nℓ×ℓ
Pour un carreau de côté ℓ, l'aire du carreau sera ℓ², et si l'on couvre la surface de Nℓ carreaux, la mesure sera
- M(ℓ) = Nℓ×ℓ²
Pour un pavé d'arrête ℓ, le volume du pavé sera ℓ3, et si l'on rempli l'objet de Nℓ pavés, la mesure sera
- M(ℓ) = Nℓ×ℓ3
On voit que la dimension est aussi l'exposant intervenant dans le calcul de la mesure.
Dans le cas d'une ligne habituelle, lorsqu'on utilise une règle de longueur ℓ divisée par deux (ou par trois, quatre,… N), on peut mettre à peu près deux (respectivement trois, quatre,… N) fois plus de fois l'étalon dans l'objet : la mesure ne change presque pas, et finalement, au fur et à mesure qu'on réduit la taille de l'étalon, on obtient une suite de mesures qui converge : la longueur exacte de la courbe est la limite de M(ℓ) lorsque ℓ tend vers 0, c'est un nombre réel.
Prenons l'exemple d'une surface ; lorsqu'on la pave des carreaux, on n'obtient qu'une approximation de son aire (on approche la surface par un polygone). Si l'on fait tenir Nℓ règles de longueur ℓ, la mesure sera
- M(ℓ) = Nℓ×ℓ 2
L'aire exacte de la courbe est la limite de M(ℓ) lorsque ℓ tend vers 0. Par contre
- M(ℓ) = Nℓ×ℓ
tend vers +∞, et
- M(ℓ) = Nℓ×ℓ 3
tend vers 0. On retrouve par le calcul ce que l'on a établi par géométrie.
Dans le cas de la courbe de von Koch, on voit bien que lorsqu'on divise l'étalon de longueur par 3, on peut mettre 4 fois plus d'étalons. Du coup, la suite de mesures de longueur
- M(ℓ/3) = Nℓ/3 ×(ℓ/3) 1 = 4Nℓ ×ℓ 1/3 = 4/3 × M(ℓ) > M(ℓ)
ne converge pas et la suite de mesures d'aire
- M(ℓ/3) = Nℓ/3 ×(ℓ/3) 2 = 4Nℓ/3 ×ℓ 2/9 = 4/9 × M(ℓ) < M(ℓ)
tend vers 0.
Mais il est possible d'imaginer une dimension fractionnaire, de faire varier de façon continue la « dimension ». Et de fait, pour la dimension
- do = log 4/log 3 ≈ 1,261 9.
on peut faire converger la mesure pour la courbe de von Koch en prenant :
- M(ℓ) = Nℓ ×ℓ do
Ceci peut être représenté de manière plus rigoureuse par la dimension d'Hausdorff-Besicovitch.
Les principales définitions
Il existe plusieurs définitions utiles pour la dimension fractale d'un ensemble. Ces définitions ne sont pas équivalentes et, dans le cas général, ne donnent donc pas toutes les mêmes valeurs. Il est conjecturé (Schroeder,1991) qu'elles sont égales dans le cas d'ensembles fractals strictement auto-similaires.
- La dimension de Hausdorff-Besicovitch est la plus courante car d'application plus universelle:
- La dimension de Minkowski-Bouligand ou Box-countig est plus simple à mettre en oeuvre pour mesurer numériquement la dimension d'une fractale, :
- La dimension d'homothétie est la traduction simple de la dimension de Hausdorff applicable aux seuls ensembles fractals a homothétie interne. La dimension d'homothétie prend sa définition par le quotient logarithmique entre un nombre d'homothéties internes d'un objet, sur l'inverse de la raison de cette homothétie. Donc,
-
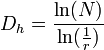
On aura donc, pour un point :
-
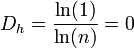
vu qu'on peut établir un point par une homothétie interne de raison n. On peut dire « un point est le produit de n homothéties internes de ce même point, de raison n ».
Avec une droite (segment), il peut s'établir avec deux homothéties internes de raison 1/2, donc
-
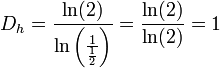
De cette façon, on trouve pour les formes et objets euclidiens, un isomorphisme entre ces deux dimensions établies. Cependant, des grandes différences se présentent avec les fractales.
Dimension topologique
La dimension topologique, définie par récurrence, associe à chaque partie P de Rn un entier, égal à la dimension algébrique si P est un sous-espace affine, à n si P est d'intérieur non vide, à 1 si P est une courbe régulière, à 2 si P est une surface régulière, etc. De manière générale elle attribue à un ensemble usuel sa dimension intuitive qui est le nombre de variables indépendantes nécessaire pour le décrire.
Dimension en algèbre commutative et en géométrie algébrique
En géométrie algébrique, l'espace topologique sous-jacent à une variété algébrique ou un schéma est relativement grossier (ne comporte pas beaucoup de parties ouvertes). La notion adéquate est celle de dimension de Krull qui mesure la longueur maximale de chaines de parties fermées irréductibles. Elle correspond à l'intuition (dimension vectorielle; dimension topologique) le cas échéant (espace affine; variétés sans point singulier sur le corps des nombres réels).
Pour un anneau commutatif unitaire A, sa dimension est la dimension de Krull du spectre premier Spec A. Par exemple, un corps est de dimension 0, alors que l'anneau des polynômes à coefficients dans un corps et à n variables est de dimension n.