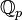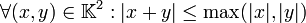Valeur absolue - Définition

Valeur absolue dans un corps

Une valeur absolue sur un corps est une application qui à tout élément x de fait correspondre un nombre réel positif noté | x | de telle sorte que  :

• (séparation) ;
• (inégalité triangulaire) ;
• 

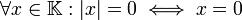
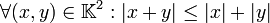
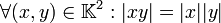
Une valeur absolue est dite ultramétrique si

C'est le cas si et seulement si cette valeur absolue est induite par une valuation à valeurs réelles.

Exemples

• Le module défini sur est bien une valeur absolue d'où le fait qu'on utilise la même notation.
• La valeur absolue p-adique défini sur le corps (p un nombre premier) est une valeur absolue ultramétrique.