Valeur absolue - Définition

Introduction

En mathématiques, la valeur absolue (parfois appelée module) d'un nombre réel est sa valeur numérique sans tenir compte de son signe. En programmation informatique, l'identificateur utilisé pour désigner la valeur absolue est usuellement abs. Il existe de nombreuses généralisations de la valeur absolue dans des espaces plus abstraits (nombre complexe, espace vectoriel ou encore corps : voir par exemple Norme). Cette notion est proche de celles de distance et de magnitude dans de nombreuses branches de la physique et des mathématiques.

Historique

Il y a eu quatre phases dans l'évolution de la notion de « valeur absolue ». Durant la première, sa définition était le « nombre sans son signe » ou la « distance à partir de zéro ». Cette définition était implicite, car il n'y avait pas eu de définition formelle.

Dans la deuxième phase, la valeur absolue était devenue une fonction, souvent utilisée dans le calcul d'erreurs. Un sens plus exact des applications de la valeur absolue à cette époque était « prendre positivement » un nombre ou « faire abstraction des signes ».

La troisième phase a découlé de la compréhension du nombre en tant que concept abstrait. La valeur absolue devint un concept spécifique défini pour chaque nombre, en plus de la méthode pour mesurer des nombres complexes. En 1821, Cauchy popularise son utilisation dans l'analyse formelle. À ce moment, il manquait une notation.

La quatrième et dernière phase découle de sa propre formalisation. Ceci était nécessaire pour l'évolution de l'analyse complexe.

Napier aurait utilisé les valeurs absolues dans l'élaboration des tables logarithmiques, alors que Descartes et Newton les auraient utilisées pour une théorie générale des équations polynomiales. Lagrange et Gauss utilisaient la valeur absolue dans la théorie des nombres pour résoudre des équations de calcul d'erreurs. Argand et Cauchy l'utilisaient pour mesurer la distance entre nombres complexes, et Cauchy l'a souvent utilisée dans l'analyse.

La fonction valeur absolue

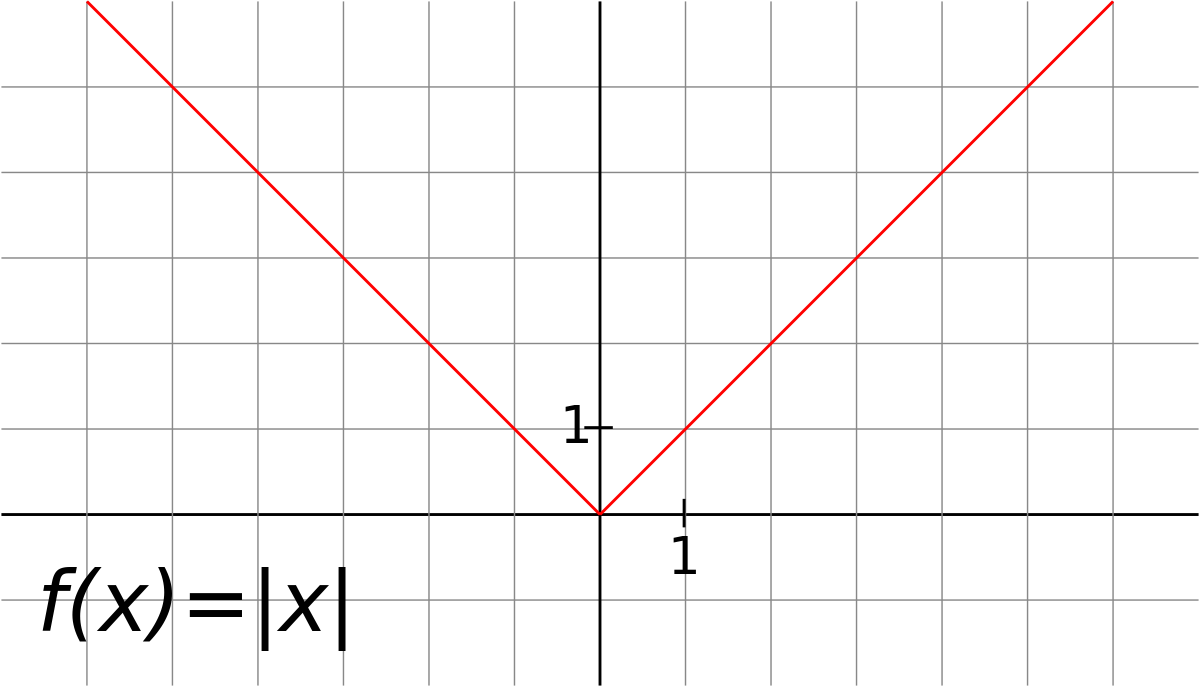
Cette fonction fait correspondre à tout x, x si celui-ci est positif ou − x si celui-ci est négatif. La fonction valeur absolue est à valeurs positives, paire.

La fonction valeur absolue f définie par f(x) = | x | est continue sur mais n'est dérivable qu'en tout point de .

La fonction valeur absolue de x

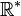
Si f est une fonction,

• la fonction g définie par g(x) = f( | x | ) est une fonction paire coïncidant avec f pour tout x de .
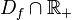
• la fonction h définie par h(x) = | f(x) | est une fonction coïncidant avec f pour tout x tel que et coïncidant avec − f pour tout x tel que

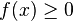
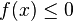
Valeur absolue d'un nombre réel

Première approche

Un nombre réel est constitué de deux parties : un signe + ou – et une valeur absolue.

+7 est constitué du signe + et de la valeur absolue 7.

–5 est constitué du signe – et de la valeur absolue 5.

La valeur absolue de +7 est donc 7, la valeur absolue de –5 est donc 5.

Comme il est fréquent de supprimer le signe lorsque celui-ci est +, on obtient alors

– la valeur absolue de 7 est 7 ;

– la valeur absolue de –5 est 5, c'est-à-dire l'opposé de –5.

D'où la définition suivante.

Définition

Pour tout nombre réel x, la valeur absolue de x (notée | x | ) est définie par :

• | x | = x, si x > 0
• | x | = − x, si x < 0
• | x | = 0, si x = 0

Nous remarquons que | x | = max( − x,x)

Propriétés

La valeur absolue possède les propriétés suivantes :

• 
• 
• 
• 
• (inégalité triangulaire)
• (deuxième inégalité triangulaire, découle de la première)
• (inégalité triangulaire généralisée à une famille finie (a_i))
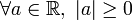
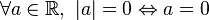
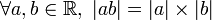
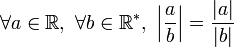
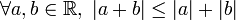
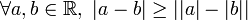
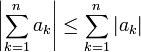
• Soit continue sur I,
• 
• 
• ou

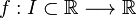
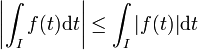
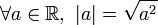
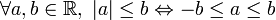
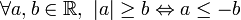
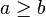
Ces dernières propriétés sont souvent utilisées dans la résolution des inéquations ; par exemple pour un x réel :

Valeur absolue et distance

Il est utile d'interpréter l'expression | x − y | comme la distance entre les deux nombres x et y sur la droite réelle.

En munissant l'ensemble des nombres réels de la distance valeur absolue, il devient un espace métrique.

La résolution d'une inéquation telle que se résout alors simplement à l'aide de la notion de distance. La solution est l'ensemble des réels dont la distance au réel 3 est inférieure ou égale à 9. C'est l'intervalle de centre 3 et de rayon 9. C'est l'intervalle [3 − 9;3 + 9] = [ − 6;12].

Extension aux nombres complexes

La même notation s'emploie pour le module d'un complexe. Ce choix est légitime parce que les deux notions coïncident pour les complexes dont la partie imaginaire est nulle. En outre, le module de la différence de deux nombres complexes z₁ = x₁ + iy₁ et z₂ = x₂ + iy₂ est la distance euclidienne des deux points et .

• 
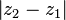
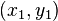
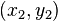
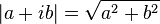
• Si b est nul, module de a = = valeur absolue de a
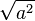
• En représentation exponentielle, si a = re^iθ alors | a | = r.