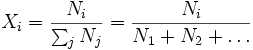Paradoxe de Gibbs - Définition

Le paradoxe de Gibbs est un pseudo-paradoxe en mécanique quantique. La mécanique quantique nous indique clairement qu'un corps pur est formé de particules indiscernables, soit des fermions si elles ont un spin demi-entier, soit des bosons si elles ont un spin entier. En tenant compte de cette indiscernabilité (peu évidente à l'époque de Gibbs vers 1900), l'entropie de Boltzmann (cf. deuxième principe de la thermodynamique, approche statistique) donne la réponse juste à ce problème.

Soit par exemple un ensemble de gaz parfaits . On mélange particules à la même température et ceci dans la somme des volumes V_i, à la même pression . On suppose également que le mélange est idéal (cf. gaz parfait). Cette opération de mélange, clairement irréversible, a provoqué une augmentation d'entropie :

,

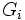
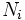
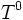
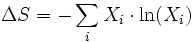
où

Démonstration

Il suffit de se souvenir que dans un mélange, l'entropie d'un gaz doit être comptée avec sa pression partielle

.

C'est en particulier vrai pour un mélange d'helium IV et d'hélium III , sauf à de trop basses température où les corrections quantiques se font sentir.