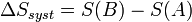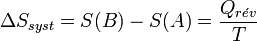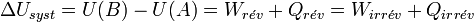Entropie - Définition

Introduction

En thermodynamique, l'entropie est une fonction d'état introduite en 1865 par Rudolf Clausius dans le cadre du deuxième principe, d'après les travaux de Sadi Carnot. Clausius a montré que le rapport Q / T (où Q est la quantité de chaleur échangée par un système à la température T) correspond, en thermodynamique classique, à la variation d'une fonction d’état qu'il a appelée entropie, S et dont l'unité est le joule par kelvin (J/K).

La thermodynamique statistique a ensuite fourni un nouvel éclairage à cette grandeur physique abstraite : elle peut être interprétée comme la mesure du degré de désordre d'un système au niveau microscopique. Plus l'entropie du système est élevée, moins ses éléments sont ordonnés, liés entre eux, capables de produire des effets mécaniques, et plus grande est la part de l'énergie inutilisée pour l'obtention d'un travail ; c'est-à-dire gaspillée de façon incohérente. Ludwig Boltzmann a exprimé l'entropie statistique en fonction du nombre Ω d’états microscopiques, ou nombre de configurations, définissant l’état d'équilibre d'un système donné au niveau macroscopique : c'est la formule de Boltzmann .

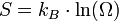
Cette nouvelle définition de l'entropie n'est pas contradictoire avec celle de Clausius. Les deux expressions de l'entropie résultent simplement de deux points de vue différents, selon que l'on considère le système thermodynamique au niveau macroscopique ou au niveau microscopique.

Plus récemment, le concept d'entropie a été généralisé, et étendu à de nombreux domaines, tels que par exemple :

• l'entropie de Shannon dans le cadre de la théorie de l'information en informatique ;
• l'entropie topologique, ainsi que l'entropie métrique de Kolmogorov-Sinaï, dans le cadre de la théorie des systèmes dynamiques en mathématiques.

L’entropie selon la thermodynamique classique

La non-conservation de l’entropie

La difficulté à donner une définition intuitive de l’entropie d’un système vient du fait qu’elle ne se conserve pas. Elle peut augmenter spontanément lors d’une transformation irréversible. En effet, selon le deuxième principe de la thermodynamique, l’entropie d’un système isolé ne peut pas diminuer, elle augmente ou elle reste constante si la transformation est réversible.

Les transformations réversibles

Une transformation affectant un système thermodynamique est dite réversible si elle est quasistatique et s’effectue sans frottement entraînant un phénomène dissipatif de chaleur. Dans ces conditions, la transformation peut être considérée comme étant constituée d’une succession d’états d’équilibre. Si on inverse le sens de la contrainte du milieu extérieur, responsable de la transformation, on repasse alors par les mêmes états d’équilibre puisqu’il n’y a pas eu de phénomènes dissipatifs. On peut alors modéliser la transformation et décrire parfaitement, à chaque instant, l’état d’équilibre du système.

La transformation réversible est donc un modèle idéal (à rapprocher du modèle idéal du gaz parfait), dont on peut se rapprocher dans les transformations réelles, en s’assurant que la transformation soit très lente, le déséquilibre des variables d'état très faible et en minimisant les frottements.

Remarque : Une transformation réversible qui serait filmée pourrait être projetée à l'envers (c'est-à-dire de la fin au début) sans que la séquence paraisse anormale. C'est par exemple le cas, en première approximation, pour une balle en caoutchouc qui rebondit une fois sur un sol dur, il serait difficile de distinguer si le film est projeté à l'endroit ou à l'envers. En toute rigueur cela est faux car les frottements lors du choc et les frottements de l'air aussi faibles soient-ils rendent le processus irréversible et après plusieurs rebonds, la balle s'arrêterait. Le film à l'envers serait alors choquant puisque la balle rebondirait de plus en plus haut !

À l'inverse, une transformation foncièrement irréversible ne permet pas de faire ce constat, comme dans le cas d'un œuf s'écrasant sur le même sol dur : projeté à l'envers on verrait l'œuf brisé se reconstituer puis monter en l'air. On trouve dans cette interprétation une manifestation de la flèche du temps.

Les transformations irréversibles

Les transformations réelles sont irréversibles à cause de phénomènes dissipatifs. Le système ne peut jamais spontanément revenir en arrière. L’énergie perdue par le système sous forme de chaleur contribue à l’augmentation du désordre global. Or le désordre est mesuré par une fonction d’état appelée entropie : S, introduite par le deuxième principe de la thermodynamique.

Alors que le premier principe est un principe de conservation de l’énergie, le deuxième principe est un principe d’évolution. Il stipule que toute transformation réelle s’effectue avec augmentation du désordre global (système + milieu extérieur) ; le désordre étant mesuré par l’entropie. On dit encore qu’il y a création d’entropie.

L’expression moderne du deuxième principe formalise cette création d’entropie :

Dans le cas de la transformation idéale réversible, il n’y a pas de création d’entropie :

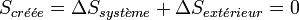
L’entropie comme monnaie d’échange

La thermodynamique classique définit l’entropie comme une grandeur extensive, ce qui signifie que l'on obtient l'entropie d'un système en faisant la somme des entropies de ses parties constituantes (par contraste, la température n’est pas une grandeur extensive parce que la température d’un système n’est pas la somme des températures de ses parties).

Tant que les transformations sont réversibles, on peut raisonner sur l’entropie comme une grandeur conservée. Comme elle peut passer d’un système à un autre ou vers le milieu extérieur, elle est une sorte de monnaie d’échange. Tout système qui gagne de l’entropie la prend à un autre ou au milieu extérieur. L'unité d’entropie, le joule par kelvin (symbole : J·K^-1) correspond à la quantité d’entropie gagnée par un système qui reçoit 1 joule de chaleur par kelvin. De façon générale, si un système reçoit joules de chaleur lors d’une transformation infinitésimale réversible à la température T, alors son entropie augmente de :

.

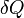
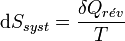
Cela devient, pour une transformation réversible effectuée à la température T constante :

.

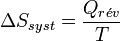
L’entropie est une fonction d’état. Cela veut dire que sa valeur est déterminée dès que l’état d’équilibre du système est établi. Comme l'entropie d'un corps pur, à la température de zéro kelvin, est nulle car le système est parfaitement ordonné, on peut construire une échelle absolue d'entropie à l'inverse des autres fonctions d'état se déduisant de l'énergie interne qui, elle, n'est pas calculable.

Si la transformation est irréversible, la chaleur mise en jeu devient car la chaleur dépend du chemin suivi. De plus, on a vu précédemment qu'il y avait création d'entropie et que le bilan entropique est positif :

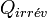
Or la chaleur fournie par le système est reçue par le milieu extérieur et donc son signe s'inverse , d'après la règle des signes.

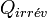
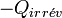
La variation de l'entropie du milieu extérieur est alors égale à : .

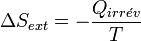
Le bilan entropique devient :

On obtient alors l'inégalité formulée par Clausius pour les transformations irréversibles :

Conséquence de l’inégalité de Clausius sur la quantité de travail fourni par un système

Considérons une transformation effectuée à la température T, qui fait passer un système thermodynamique d’un état initial A à un état final B d’équilibre.

La variation d’entropie du système, associée à cette transformation, peut s'écrire :

On peut procéder de façon réversible ou bien de façon irréversible. Si la variation de la fonction d'état entropie sera la même, il n’en est pas de même pour la chaleur Q et le travail W qui dépendent du chemin suivi et seront donc différents : et .

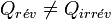
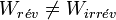
Appliquons le deuxième principe :

• 
• 

d’où .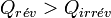

Appliquons le premier principe de conservation de l’énergie interne U :

On déduit que .

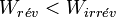
Pour un système (moteur thermique, moteur électrique…) dont la fonction est de fournir du travail au milieu extérieur, le travail fourni est compté négativement d’après la règle des signes : W < 0

Donc ce qui compte c’est la valeur absolue du travail fourni et l’inégalité s’inverse :

On en déduit que la quantité de travail utile fournie par un système est plus importante lorsque la transformation est réversible.

Remarques :

• Les frottements étant la principale cause d’irréversibilité, on comprend pourquoi on essaye de les minimiser ; c’est le but de la lubrification des pièces en contact et en mouvement dans un ensemble mécanique.
• La vitesse est un facteur d’irréversibilité : la récupération de travail mécanique décroît à mesure que la vitesse d'un véhicule s'accroît. Ainsi, pour une même quantité de carburant, plus un véhicule se déplacera rapidement, plus la distance qu'il pourra parcourir sera réduite.
• Une pile électrique fournit plus de travail électrique si son fonctionnement se rapproche de la réversibilité (faible tension et faible courant de fonctionnement). En revanche si on court-circuite les électrodes, on ne récupère pratiquement que de la chaleur !