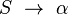Analyse Earley - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
L'algorithme d'Earley est un algorithme non déterministe d'analyse syntaxique pour les grammaires non contextuelles. Il a été décrit pour la première fois par Jay Earley. Il se range, aux côtés des algorithmes CYK et GLR, parmi les algorithmes qui font usage de la notion de partage (de calculs et de structures) et qui construisent toutes les analyses possibles d'une phrase (et pas seulement une de ces analyses). Ce sont donc des algorithmes non-déterministes qui font usage d'idées venues du domaine de la programmation dynamique.
On peut construire un analyseur Earley pour toute grammaire non contextuelle. Il s'exécute en temps cubique (O(n3), où n est la longueur de la chaîne d'entrée, voire la taille du DAG d'entrée, l'algorithme pouvant aisément s'étendre à l'analyse de DAG). Pour une grammaire non ambiguë, l'analyse Earley s'effectue en temps quadratique (O(n2)).
L'algorithme d'Earley
Considérons une grammaire non contextuelle ainsi qu'une chaîne d'entrée de longueur n notée

Items Earley et tables Earley
L'algorithme d'Earley fait usage de ce que l'on appelle des items Earley, ou plus simplement des items. Un item est entièrement défini par une production de la grammaire, un entier i, appelé indice de début, tel que
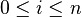
![[i]\ A\ \rightarrow\ \alpha \bullet \beta](https://static.techno-science.net/illustration/Definitions/autres/7/7d4f628f162f25e63bbbb87ccfa237d6_ab867f607886d8dbe7533d4de4480fb0.png)
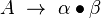
Supposons que l'on soit à la j-ième étape (et donc à la position j de la chaîne d'entrée). Un item est dit j-valide (ou valide s'il n'y a pas d'ambiguïté) s'il représente une production dont on est en train d'essayer de faire dériver une sous-chaîne
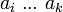
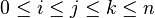

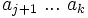
On définit la table T[j] comme l'ensemble des items j-valides. Un item de la table T[j] est donc valide s'il représente une situation où l'on est à la j-ième étape (on a reconnu les j premiers symboles de la chaîne d'entrée, c'est-à-dire le préfixe

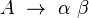
![[i]\ A\ \rightarrow\ \bullet \beta](https://static.techno-science.net/illustration/Definitions/autres/a/a4e8f1e8e5e88499faa0fda9c455d97d_f9648f79303585f13359eaac72d6e054.png)
![[i]\ A\ \rightarrow\ \alpha \bullet](https://static.techno-science.net/illustration/Definitions/autres/9/9e8ea333878c8e87c49ec447ff6ea6fb_52120427180263afe8d511f6150b9461.png)

Supposons que S soit l'axiome de la grammaire. Les items de la forme
![[0]\ S\ \rightarrow\ \bullet \alpha](https://static.techno-science.net/illustration/Definitions/autres/9/9884f5a0199394ac69f2eae6f487b683_651d4702becc631587fdfe2ad8515175.png)
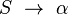
![[0] S \ \rightarrow\ \alpha \bullet](https://static.techno-science.net/illustration/Definitions/autres/9/9edae3397db26799c5b74042a2ff6853_dbab2c8b8160d6f4867078ac3b78fafd.png)
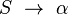
Algorithme d'analyse
Le but de l'algorithme est donc de calculer en n + 1 étapes tous les items valides et seulement les items valides. La j-ième étape va donc être chargée de construire la table T[j] en construisant tous les items j-valides, et seulement ceux-ci.
Chacune des étapes exécute trois types d'opérations, nommées Lecture, Prédiction et Complétion (en anglais, respectivement Scanner, Predictor, Completor). À l'exception de l'étape 0, qui commence par la construction des items de départ comme dit ci-dessus (construction de la table T[0]), la j-ième étape commence par les opérations de Lecture. Le but de ces opérations est de faire avancer les points dans les items de la table précédente où le point est juste avant un terminal qui est précisément aj. Autrement dit, pour tout item de T[j − 1] de la forme
![[i]\ A\ \rightarrow\ \alpha \bullet a_j\ \beta](https://static.techno-science.net/illustration/Definitions/autres/8/83ac930f07d8e7455870680e74ffa70c_3b67a71256a292ee15e4cbde37db8088.png)
![[i]\ A\ \rightarrow\ \alpha\ a_j \bullet \beta](https://static.techno-science.net/illustration/Definitions/autres/e/e29b8059c6bc54752977f634cd01ac60_693691f439cdd5af2f71bac8fb92cc61.png)
- Soit β commence par un terminal, et la phase Lecture de l'étape j + 1 s'en occupera plus tard. On ne fait donc rien pour le moment.
- Soit β commence par un non terminal B. Dans ce cas, il faut lancer (prédire) la reconnaissance du non-terminal B à partir de la position courante j. On rajoute donc dans T[j], pour toutes les règles
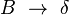
![[j]\ B\ \rightarrow\ \bullet \delta](https://static.techno-science.net/illustration/Definitions/autres/6/68f768c3977b088da219c7a218399df9_0a169941a2349ea29593fa3cca91b86f.png)
- Soit β est vide. On a donc terminé et réussi la reconnaissance de A entre les positions i et j. On va donc chercher tous les items qui avaient lancé la reconnaissance de A à partir de la position i, c'est-à-dire les items de la table T[i] de la forme
![[k]\ C\ \rightarrow\ \delta \bullet\ A\ \gamma](https://static.techno-science.net/illustration/Definitions/autres/5/59a6d6efa750c1bcd1634e8d1fb8d95f_f81cec895b9551b687205077df3fdd62.png)
![[k]\ C\ \rightarrow\ \delta\ A\ \bullet \gamma](https://static.techno-science.net/illustration/Definitions/autres/0/083039cdd37c3039bab6515cdcdc1c6b_713308a54e47526837a49100713a7752.png)
L'exécution d'une Prédiction ou d'une Complétion ajoute un item dans la table courante (la table T[j]). Ce nouvel item peut lui-même permettre de nouvelles Prédictions et de nouvelles Complétions. Celles-ci sont exécutées, et ainsi de suite jusqu'à ce que la table courante soit stable (et donc complète). Toutes ces opérations peuvent avoir pour effet de faire avancer le point dans des règles, si les non-terminaux que l'on franchit peuvent dériver dans le vide. Mais elles ne font pas avancer le point dans la chaîne d'entrée: on reste à la position j, et on ne remplit que la table T[j].
On peut se convaincre facilement (quitte à lire une preuve dans la littérature) que l'on ne construit ainsi que des items valides destinés à la table T[j], mais qu'on les construit tous.
Une fois que l'on ne peut plus construire de nouvel item pour la table T[j], on passe à l'étape j + 1. L'analyse réussit si on arrive de cette façon à exécuter les n étapes et si on obtient une table T[n] comprenant des items de la forme
![[0] S\ \rightarrow\ \alpha \bullet](https://static.techno-science.net/illustration/Definitions/autres/9/9edae3397db26799c5b74042a2ff6853_dbab2c8b8160d6f4867078ac3b78fafd.png)