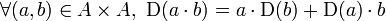Anneau (mathématiques) - Définition
La liste des auteurs de cet article est disponible ici.
Classification des anneaux remarquables
La théorie des anneaux étant une branche très riche de l'algèbre, il est difficile de se repérer dans la jungle des anneaux particuliers. Le schéma ci-dessous donne une illustration partielle de leur hiérarchie - une flèche fait passer du général au particulier.
On peut remarquer que l'anneau qui se détache de cette hiérarchie est l'anneau euclidien : c'est celui qui va posséder le plus de propriétés.
Dérivation
Une dérivation d'un anneau A à valeurs dans un A-module M est une application additive de A dans M
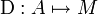
Cette notion est en particulier vérifiée par la dérivée d'une fonction (de variable réelle, par exemple); elle en est une généralisation utilisée en géométrie algébrique et en calcul différentiel sur les variétés (par exemple pour définir le crochet de Lie). Toute application de dérivation vérifie la formule de Leibniz.