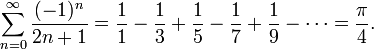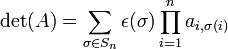Formule de Leibniz - Définition
Plusieurs formules portent le nom de Formule de Leibniz
Dérivée du produit de deux fonctions dérivables
Le produit de deux fonctions f et g dérivables (sur 
ou 
) à l'ordre n est dérivable à l'ordre n. Sa dérivée d'ordre n est donnée par la formule :
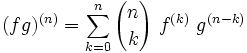
où les nombres entiers 
sont les coefficients binomiaux.
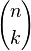
Cette formule, proche dans sa forme de la formule du binôme de Newton, se prouve par récurrence de la même façon que cette dernière. On peut d'ailleurs en déduire la formule du binôme de Newton en choisissant f(x) = eax et g(x) = ebx.
Elle peut s'énoncer également pour des polynômes à coefficients dans un anneau commutatif quelconque et pour toute dérivation définie sur un anneau.
Formule donnant π / 4
De nombreuses formules permettent de déterminer une valeur de π / 4. L'une d'entre elles vous est présentée ici. Cette formule est :
(Démonstration de la formule de Leibniz)
Elle a été découverte en Occident au XVIIème, mais apparaît en fait chez Madhava, mathématicien indien de la province de Kerala vers 1400.
Déterminant d'une matrice carrée
Le déterminant d'une matrice carrée A = (aij) d’ordre n est le nombre noté det(A) égal à :
où Sn est l’ensemble des permutations de {1, 2, …, n} et pour une permutation σ de Sn, ε(σ) désigne sa signature ; égale à 1 si la permutation est paire et -1 si la permutation est impaire.