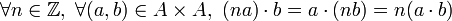Anneau (mathématiques) - Définition

Introduction

En algèbre générale, un anneau est une structure algébrique sur laquelle deux opérations satisfont certaines des propriétés de l'addition et la multiplication des nombres.

Aspect historique

L'étude des corps et des anneaux trouve son origine dans l'école allemande du XIX^e siècle. Elle est développée par les mathématiciens Kummer, Dedekind, Kronecker et Hilbert. Elle naît de l'étude des équations algébriques, des nombres algébriques et de la recherche d'une démonstration du grand théorème de Fermat. Elle conduira à un développement important de l'algèbre générale et de la géométrie algébrique.

Dans le X^e Supplément de sa seconde édition des Leçons sur la théorie des nombres de Dirichlet, en 1871, Dedekind considère, à côté de la notion de corps (Körper), l'anneau des entiers d'un corps de nombres algébriques ; il introduira un peu plus tard d'autres anneaux qu'il appelle ordres (Ordnung). Mais c'est David Hilbert qui emploie le terme d'anneau (Ring) pour définir ce qui est toujours à l'époque un anneau commutatif unitaire, dans son Rapport sur les nombres (Zahlbericht) de 1897 pour la Deutsche Mathematiker-Vereinigung.

Opérations sur les éléments d'un anneau

Puissances dans un anneau

Soit n un entier naturel supérieur à 1, x un élément de l'anneau A, on note xⁿ pour désigner l’élément de A défini par récurrence à partir de :

x¹ = x et x^{n + 1} = xⁿ.x.

On a :

x^m.xⁿ = x^{m + n}.

Pour tout entier naturel non nul n, xⁿ résulte de n-1 associations de la seconde loi de composition interne associative ·, en utilisant n valeurs successives toutes égales à x (l’ordre de ces compositions est sans importance car elles sont associatives)

xⁿ = x.x....x.

Si l'anneau A est unitaire, on pose habituellement x⁰ = 1_A.

Eléments permutables dans un anneau et anneaux commutatifs

Si xy=yx, on dit que x et y sont permutables et alors (xy)ⁿ = xⁿ.yⁿ.

• Anneau commutatif : un anneau est commutatif si sa seconde loi est aussi commutative, c'est-à-dire si tous ses éléments sont permutables.

Voir article détaillé : Anneau commutatif

Convention : Le terme « anneau » est souvent employé pour désigner un anneau commutatif unitaire. Il faut donc prêter garde au contexte dans lequel ce terme est employé.

Multiplication par un entier relatif

Précisons tout de suite que cette multiplication ne fait pas partie de la structure de l'anneau, mais elle apparaît de façon naturelle pour tout anneau. Il s'agit tout simplement de la multiplication par un entier appliquée au groupe additif de l'anneau. L'élément na est défini par

• si avec n termes a
• si
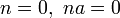
• si

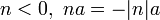
De plus, cette loi externe est compatible avec la multiplication de l'anneau :

Cela confère alors à l'anneau une structure de -algèbre associative. En particulier, si l'anneau est unitaire, on peut multiplier son unité par tout entier, et cela définit une application de Z dans A . Il est clair, d'après sa définition, que cette application est le seul morphisme d'anneaux unitaires de Z vers A. On peut alors définir la caractéristique de l'anneau comme l'entier naturel n qui engendre le noyau de ce morphisme. En effet, le noyau de ce morphisme est un idéal de Z et s'écrit alors nZ.

Cette structure additionnelle est très utilisée pour les différentes théories de cohomologie.

Formule du binôme

Voir Formule du binôme de Newton.

Cette formule est applicable à tout couple d'éléments permutables.

Elle se généralise à toute famille finie d'éléments permutables deux à deux : Formule du multinôme.