Automate à pile - Définition

Introduction

Un automate à pile est une machine abstraite utilisée en informatique théorique et, plus précisément, en théorie des automates.

Un automate à pile est semblable à un automate fini mais il dispose également d'une pile. Ainsi, un automate à pile prend en entrée un mot et réalise une série de transitions, chacune consistant à lire une lettre de du mot ou à réaliser des opérations sur la pile. Les transitions effectuées dépendent des lettres du mot et du sommet de la pile. Selon l'état de l'automate à la fin du calcul, le mot peut être accepté ou refusé.

La puissance de calcul des automates à piles correspond aux langages non-contextuels soit ceux qui peuvent être décrits par une grammaire hors-contexte.

Définitions formelles

Automate à pile non déterministe

Un automate à pile (non déterministe) est un 7-uplet , où

• est l'ensemble d'états,
• est l'alphabet d'entrée,
• est l'alphabet de pile,
• est la fonction de transition (la notation désignant l'ensemble des parties),
• est le symbole de fond de pile,
• est l'état initial,
• est l'ensemble des états terminaux.

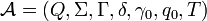
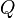
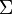
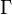
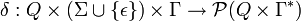
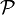
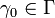
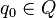
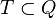
Une configuration de l'automate est un triplet . Un calcul de l'automate sur un mot est une série de transitions à partir de la configuration (q₀,w,γ₀). À partir d'une configuration (q,σw,γβ), où σ et γ sont des lettres de Σ et Γ, les transitions possibles sont :

• lorsque ,
• lorsque .

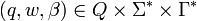
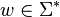
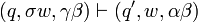
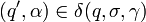
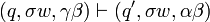
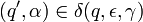
On dit qu'un mot est accepté par l'automate s'il existe une série de transitions qui conduit à une configuration acceptante, notion qui peut être définie de deux façons :

• Pour les automates à reconnaissance par pile vide, les configurations acceptantes sont les configurations de la forme (q,ε,ε) où est un état quelconque. Autrement dit, il est possible d'arriver à vider entièrement la pile au moment où on termine la lecture du mot.
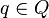
• Pour les automates à reconnaissance par état final, les configurations acceptantes sont les configurations de la forme (q,ε,β) où est un état final.

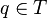
Dans le cas non déterministe, cette distinction n'a pas d'importance car les deux types d'automates sont équivalents.

Le langage reconnu par l'automate est l'ensemble des mots de Σ ^* qui sont acceptés.

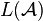
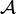
Automate à pile déterministe

Un automate à pile déterministe est défini de la même manière qu'un automate à pile non déterministe, à l'exception de la fonction de transition. Dans le cas déterministe, δ est une fonction partielle . De plus, lorsque δ(q,ε,γ) est définie, alors δ(q,σ,γ) ne peut être définie pour aucun . Ainsi, au plus une transition est possible à partir de n'importe quelle configuration.

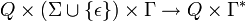
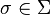
On distingue de même deux types de reconnaissance, par état final ou par pile vide. Les automates déterministes avec reconnaissance par état final sont plus puissants que les automates avec reconnaissance par pile vide. Plus précisément, un langage L peut être reconnu par le second type d'automate s'il peut être reconnu par un automate du premier type et qu'aucun mot du L n'est préfixe d'un autre. Par exemple, le langage aⁿbⁿ(n > 0) est reconnu par les deux types d'automates déterministes, mais le langage aⁿ ne l'est que par automate déterministe par état final.

Propriétés

Chaque langage défini par une grammaire non contextuelle est reconnu par un automate à pile et réciproquement.

En conséquence, le problème de l'appartenance d'un mot à un langage non contextuelle est décidable : il existe un algorithme qui, étant donnés la description d'une grammaire non contextuelle et un mot, répond en temps fini à la question de l'appartenance de ce mot au langage défini par cette grammaire (plus précisément, on peut le tester en temps O(n³) pour un mot de longueur n, grâce à l'algorithme CYK).

La classe des langages rationnels (reconnus par automate fini) est strictement incluse dans la classe des langages algébriques déterministes (reconnus par automate à pile déterministe par état final), elle même strictement incluse dans la classe des langages algébriques (reconnus par automate à pile non déterministe). Par exemple, le langage aⁿbⁿ est algébrique déterministe mais non rationnel, et le langage des mots palindromes est algébrique mais pas algébrique déterministe. Certains langages ne sont pas reconnus par automate à pile, par exemple aⁿbⁿcⁿ (on peut le montrer à l'aide du lemme d'Ogden).